一、画图基本代码
1、引入库
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['figure.dpi'] = 300
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']2、直方分布图
plt.figure(figsize=(10, 6))
data = [np.log10(a) for a in list_conformity_real] # 对数直方图,以10为底,np.log(a)默认以e为底
min_val, max_val = np.min(data), np.max(data)
bins1 = np.linspace(min_val, max_val, num=30)
sns.histplot(data, bins=bins1, color="red", alpha=0.7, label='real_data') # stat='count'默认是频数 , stat="density"画概率密度
# plt.hist(l1, bins=30, range=(min_val, max_val), color='red', edgecolor='black', alpha=0.7)
# sns是升级的直方图,plt.hist是基础直方图3、互补累计分布图
from collections import Counter
plt.figure(figsize=(10, 6))
count = Counter(list_conformity_real) # 计算出现频次
x = sorted(count.keys())
y = [count[key] for key in x]
y_cu = [] # 互补累积
pro = 1
total = sum(y)
for i in range(len(y)):
y_cu.append(pro)
pro -= y[i]/total
plt.scatter(x, y_cu, c='red', label='真实数据')
plt.title('从众性互补累积分布图', fontsize=16)
plt.xscale('log', base=10) # 默认底数为10,也可以设置base=np.e以e为底数
plt.yscale('log', base=10)
plt.xlabel('从众性', fontsize=14)
plt.ylabel('概率', fontsize=14)
# plt.ylim(bottom=1e-6) # 设置y轴下限
plt.show()4、拟合正态分布并检验
from scipy.stats import norm
from scipy.stats import shapiro, kstest
import statsmodels.api as sm
mean, std = norm.fit(data) # 正态分布拟合
xn = np.linspace(min(data), max(data), 1000)
pn = norm.pdf(xn, mean, std)
# plt.plot(xn, pn, 'b-', label='Normal fit') # 概率密度拟合
bin_width = bins1[1] - bins1[0] # 计算每个bin的宽度
pn_scaled = pn * len(data) * bin_width # 概率密度转为频数
plt.plot(xn, pn_scaled, 'b-', label='Normal fit') # 频数拟合直方分布
# 可以用 Shapiro-Wilk 检验或 Kolmogorov-Smirnov 检验判断正态性:
stat, p_value = shapiro(data)
print('Shapiro-Wilk test p-value:', p_value)
# 如果 p 值大于 0.05,则不能拒绝正态分布假设,说明对数数据近似正态
# 用 statsmodels 画 Q-Q 图,直观判断数据与正态分布的吻合度:
sm.qqplot(np.array(data), line='45')
plt.show()
# 点大致沿对角线分布说明近似正态二、ArcGIS操作
1、获得城市矢量底图的步骤
打开arcmap-添加数据-AddBasemap-选择一个合适的风格,然后选定自己想要的地区(查找-输入地区名称)-文件-导出地图-emp/emf
三、画图示例图
1、折线图
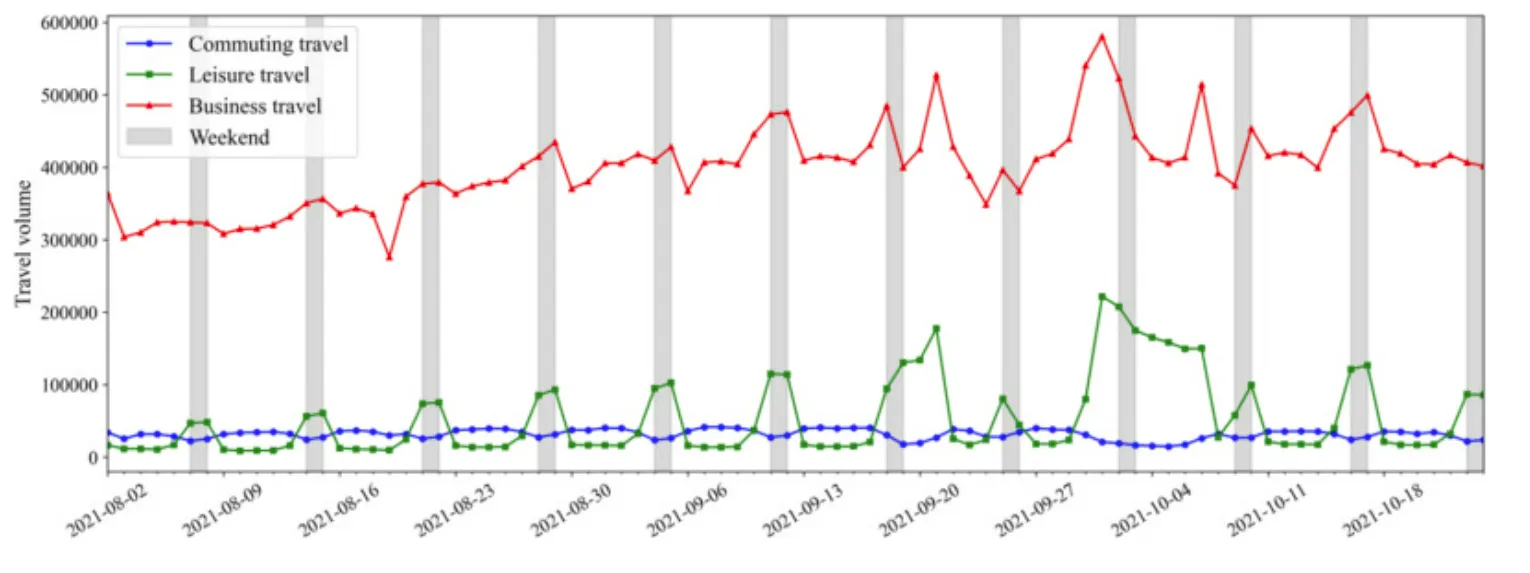
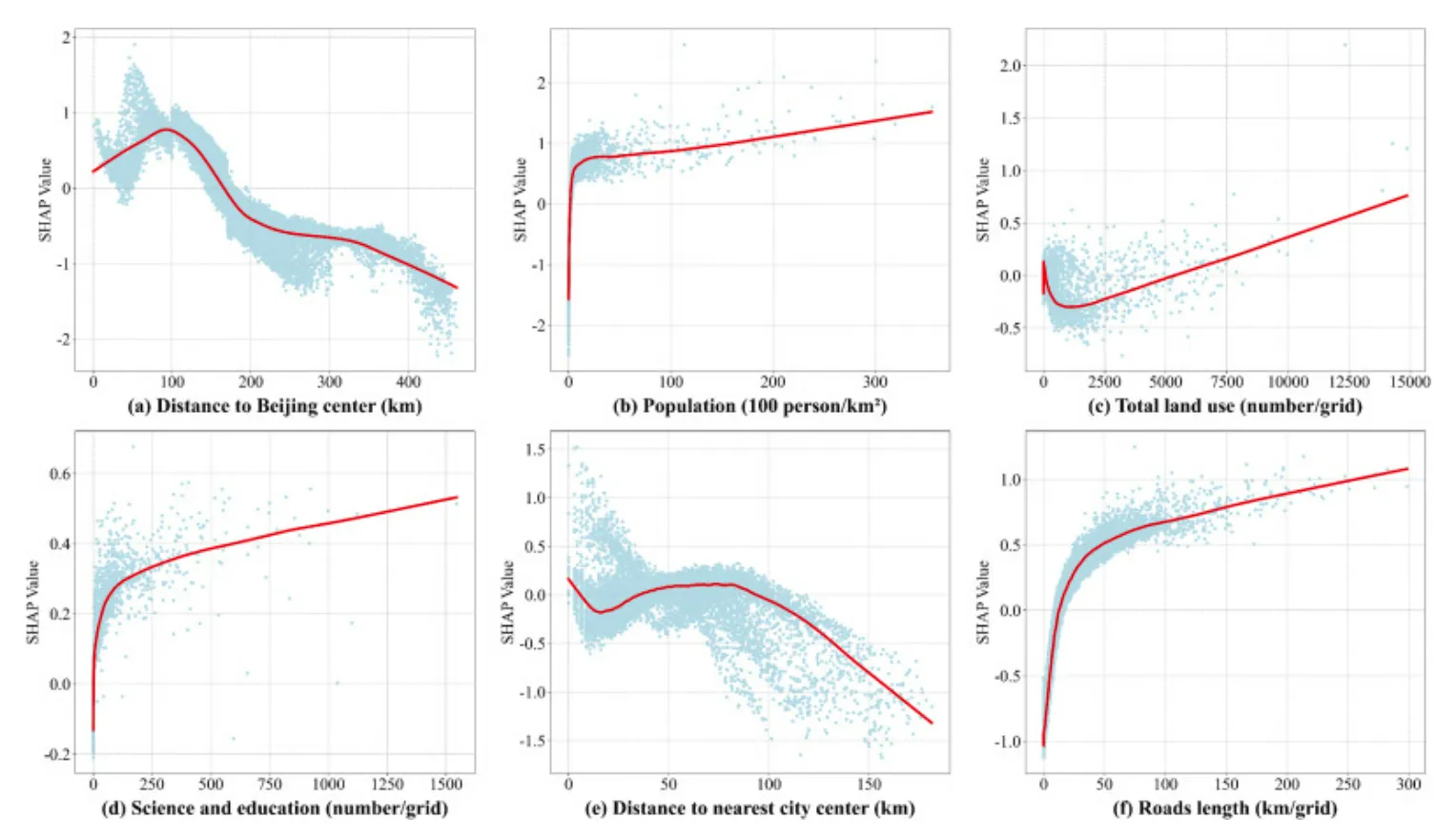
2、柱状图
3、饼图
4、散点图
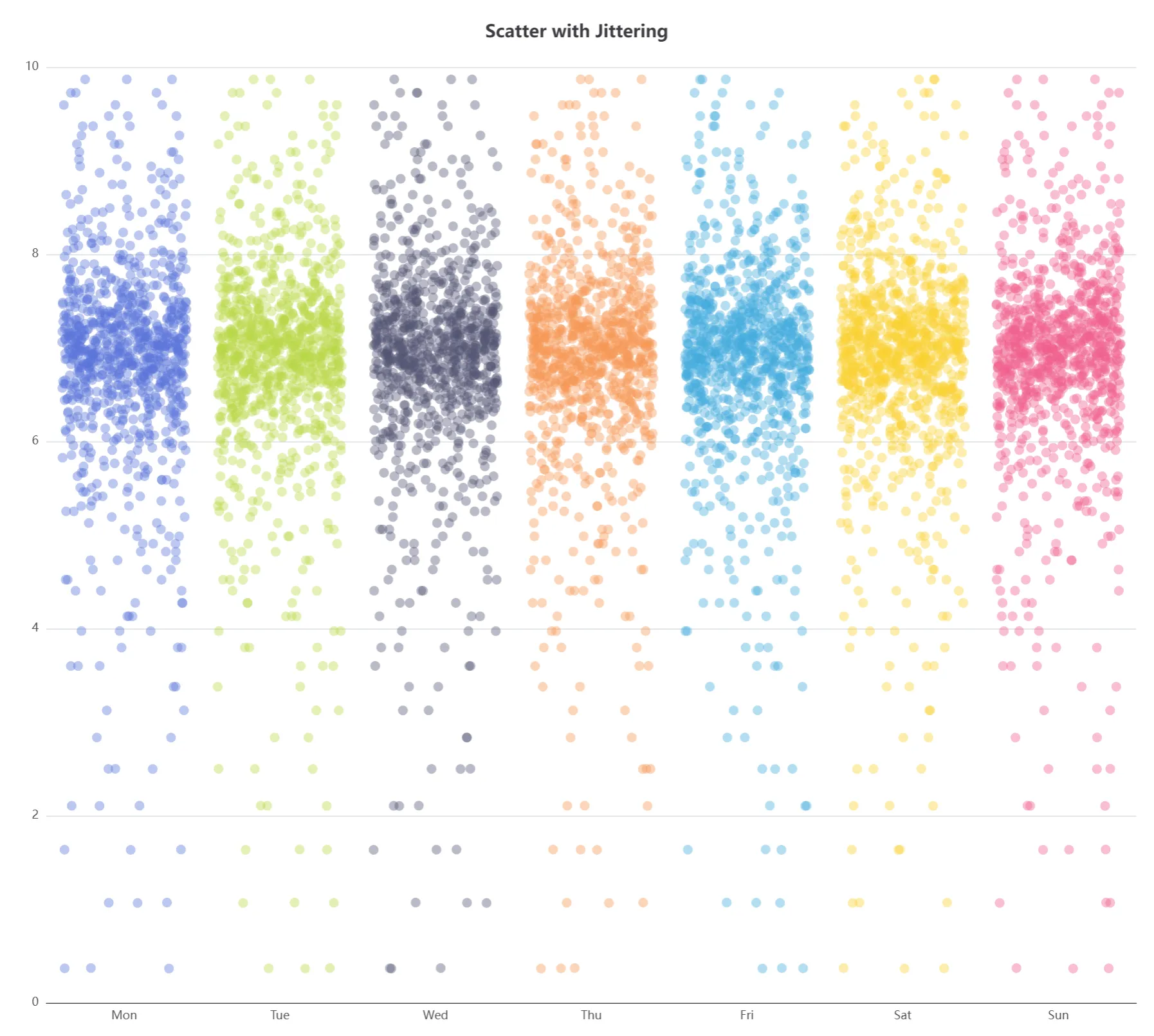
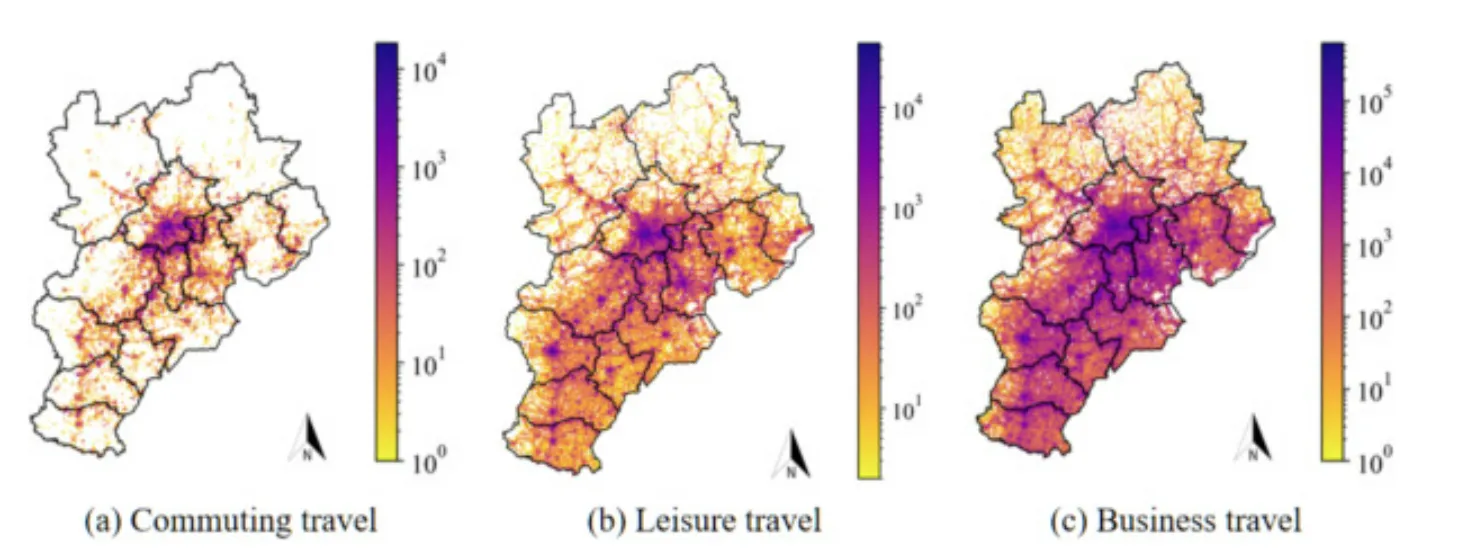
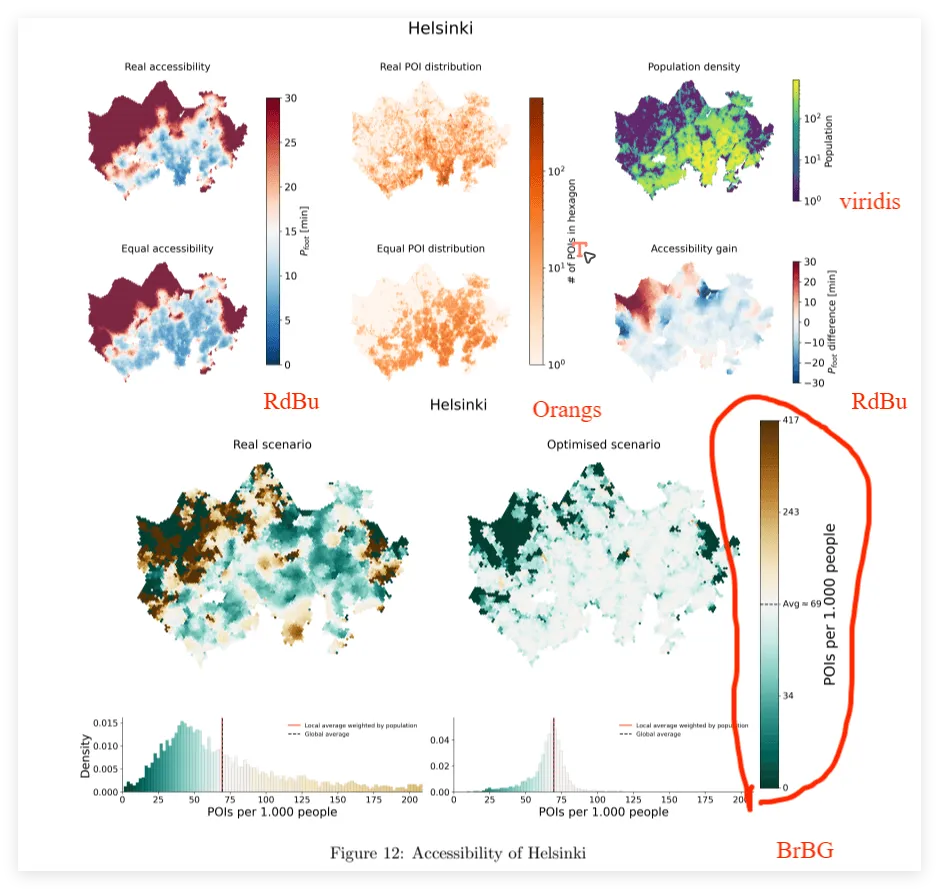
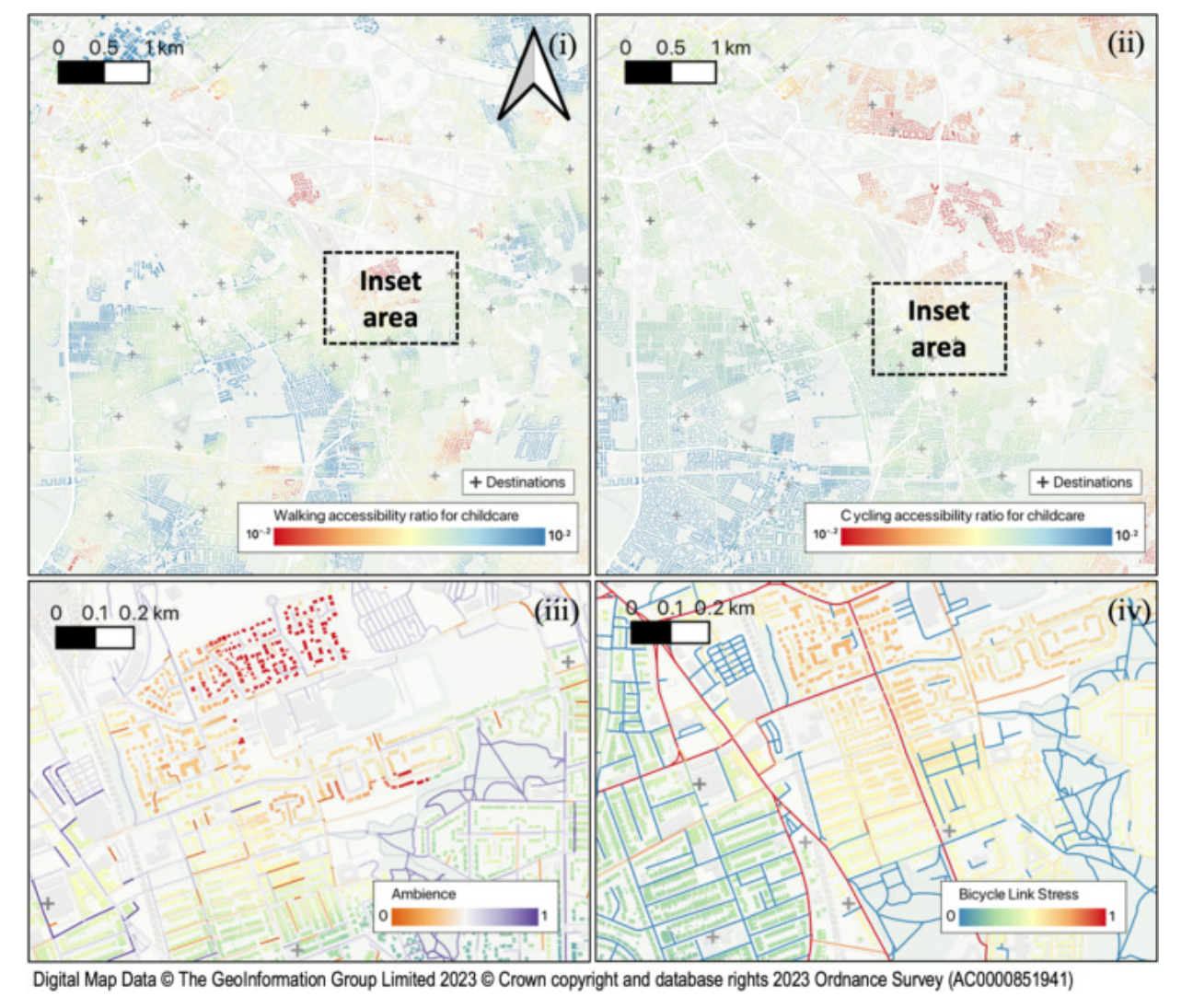
5、地图
6、雷达图
7、箱线图
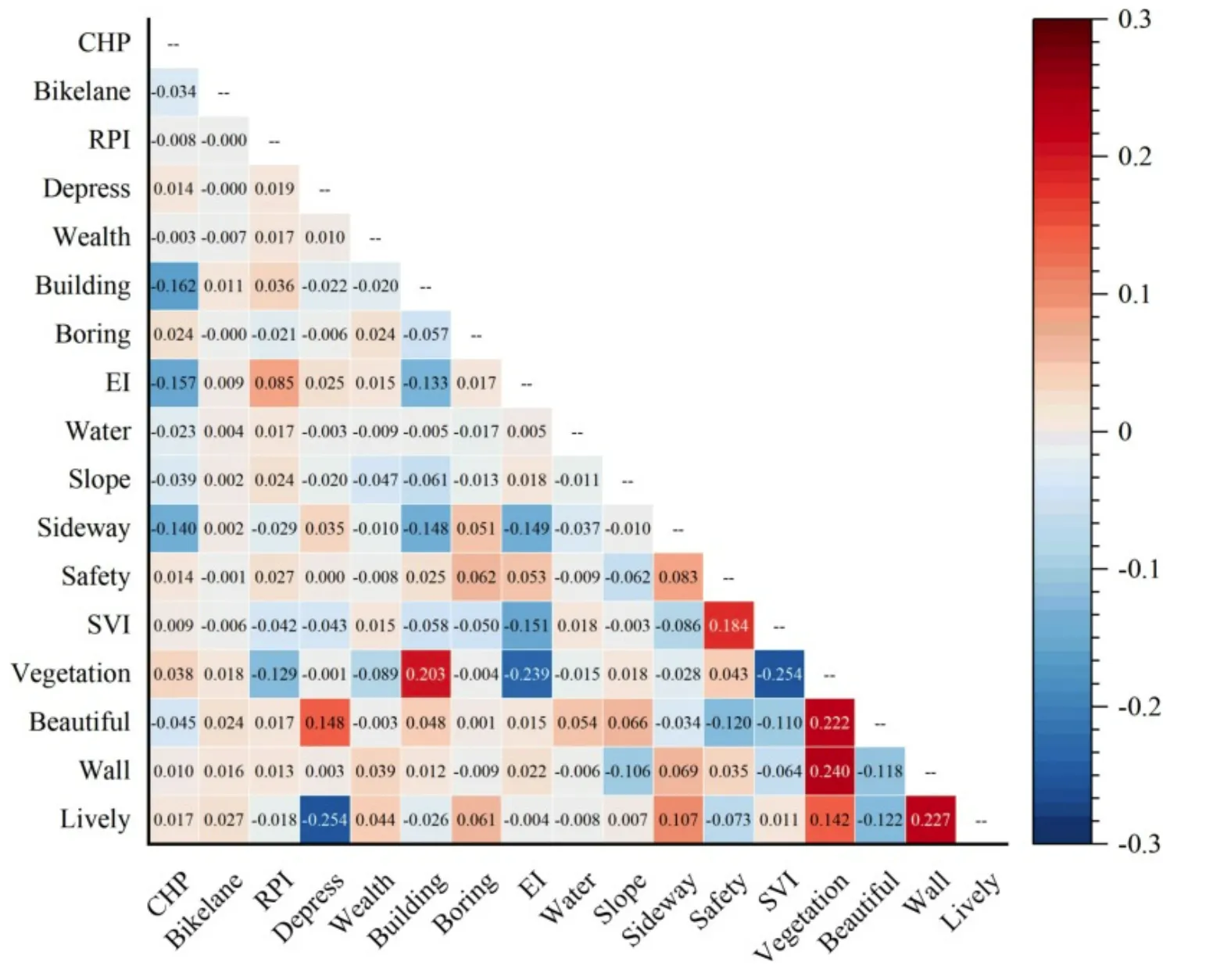
8、热力图
9、关系图

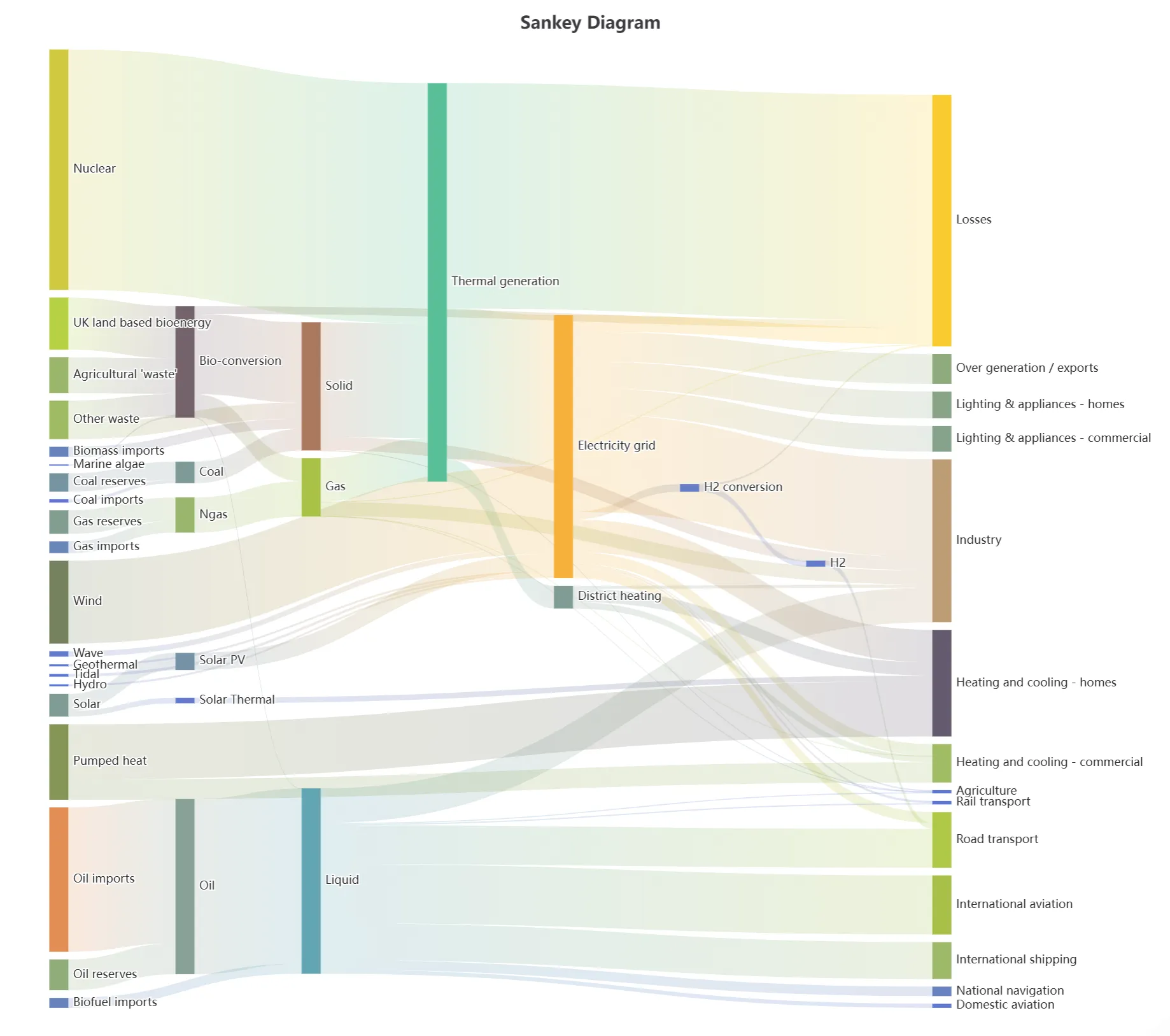
10、桑基图