一、聚类算法
(一)聚合聚类
聚合聚类(Agglomerative Clustering)是一种自底向上的聚类方法。它从数据点(或称为观测值)的集合开始,然后将这些点视为初始的簇。接着,算法逐步合并这些簇,直到满足某个停止条件,如达到预设的簇数量或达到某个特定的簇大小。在这个过程中,算法通过计算簇之间的距离来确定哪些簇应该被合并。
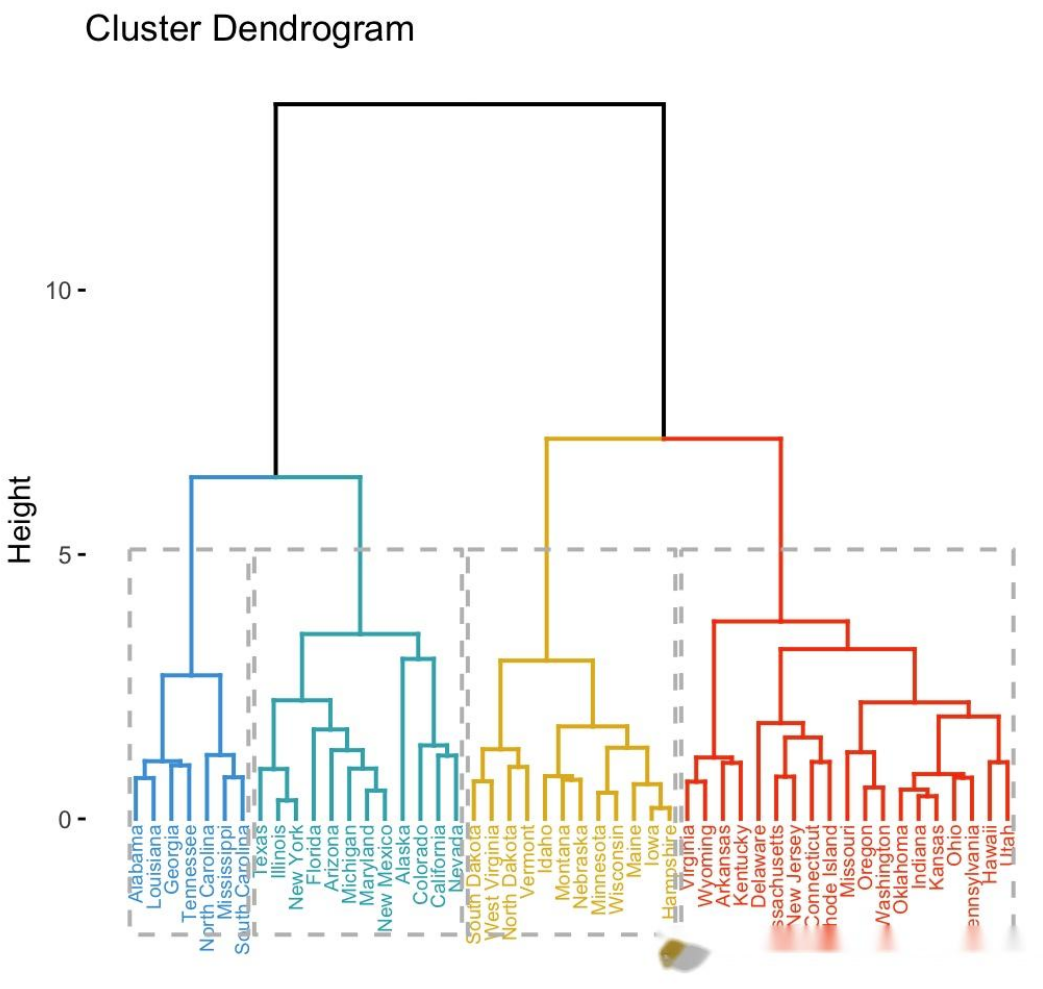
1、步骤
- 初始化:每个数据点被视为一个簇。
- 合并:根据某种距离度量(如欧氏距离、余弦相似度等),将最近的簇合并为一个新的簇。
- 重复:重复步骤2,直到满足停止条件。
- 输出:返回合并后的簇结果。
2、优缺点
- 层次结构:能够生成数据的层次结构或嵌套聚类,这在某些应用中非常有用。
- 可解释性:由于是自底向上的方法,可以更容易地解释和可视化结果。
- 处理大型数据集:由于不需要一次性处理所有数据,因此可以有效地处理大型数据集。
- 时间复杂度:随着数据集规模的增加,时间复杂度可能会迅速增加。
- 不平衡簇:可能产生不平衡的簇,即某些簇包含大量数据点,而其他簇则包含很少的数据点。
- 初始化敏感:对初始化的选择敏感,可能会导致不同的聚类结果。
3、使用场景
- 层次聚类:适用于需要层次结构的聚类任务,如市场细分或社交网络分析。
- 异常检测:可以通过观察聚类结果中的离群点来检测异常值。
- 数据预处理:在某些机器学习任务中,可以使用聚合聚类作为预处理步骤来简化数据或提取特征。
4、代码
from sklearn.cluster import AgglomerativeClustering # 导入AgglomerativeClustering类
from sklearn import datasets # 导入datasets用于生成样本数据
from sklearn.preprocessing import StandardScaler # 导入StandardScaler进行标准化处理
import matplotlib.pyplot as plt # 导入绘图库
iris = datasets.load_iris() # 生成样本数据
X = iris["data"] # 使用Iris数据集作为示例 # 提取特征矩阵
scaler = StandardScaler() # 数据标准化
X = scaler.fit_transform(X) # 对数据进行标准化处理 # 设置聚类数
n_clusters = 2 # 根据需求设置聚类数
clustering = AgglomerativeClustering(n_clusters=n_clusters) # 创建AgglomerativeClustering对象并拟合数据
labels = clustering.fit_predict(X) # 获取每个样本点的聚类标签
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis') # 使用viridis色彩映射绘制结果图
plt.show() # 显示结果图 ```(二)DBSCAN 聚类
Density-Based Spatial Clustering of Applications with Noise是一种基于密度的聚类方法。它的主要思想是:一个簇是由一个密度足够大的区域所组成的,并且这个区域是核心对象所连接的稠密区域。DBSCAN将簇定义为具有足够高密度的区域,并且通过噪声点将簇与相邻的密度区域分开。
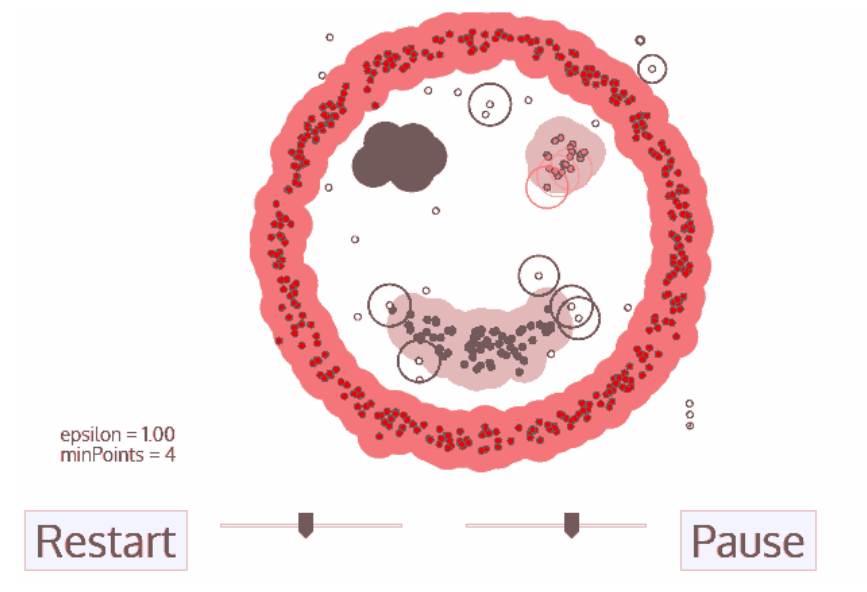
1、步骤
- 初始化:选择一个未被访问过的点作为当前点。
- 密度估计:如果当前点的ε-邻域内的点数量大于等于MinPts,则当前点为核心点。否则,当前点为噪声点。
- 扩展簇:从核心点开始,将其标记为簇的一部分,并递归地访问其ε-邻域内的所有点。如果某个点的ε-邻域内的点数量大于等于MinPts,则该点为核心点,并将其标记为已访问。
- 重复:重复步骤2和3,直到所有点都被访问。
- 输出:返回所有簇的结果。
2、优缺点
- 密度敏感:能够发现任何形状的簇,并处理异常值和噪声。
- 可扩展性:对于大规模数据集,DBSCAN具有较好的可扩展性。
- 无需预设簇数量:与其他基于距离的聚类方法相比,DBSCAN不需要预设簇的数量。
- 参数敏感:对参数ε和MinPts的选择较为敏感,不同的参数值可能会导致不同的聚类结果。
- 计算量大:对于高维数据,DBSCAN的计算量可能会很大。
- 对噪声和异常值敏感:如果数据集中存在大量噪声或异常值,可能会影响聚类的效果。
3、使用场景
- 异常检测:由于DBSCAN对噪声和异常值敏感,因此可以用于异常检测任务。
- 任意形状的簇:对于需要发现任意形状的簇的应用,如社交网络分析、图像分割等,DBSCAN是一个很好的选择。
- 数据预处理:在某些机器学习任务中,可以使用DBSCAN对数据进行预处理,以便进一步的分析或分类。
4、代码
from sklearn.cluster import DBSCAN # 导入DBSCAN聚类算法
from sklearn import datasets # 导入datasets用于生成样本数据
importmatplotlib.pyplotasplt #导入绘图库
iris = datasets.load_iris() # 使用Iris数据集作为示例
X = iris["data"] # 提取特征矩阵
dbscan = DBSCAN(eps=0.3, min_samples=5) # 创建DBSCAN对象并拟合数据 eps是邻域半径,min_samples是形成核心对象的最小点数
labels = dbscan.fit_predict(X) # 获取每个样本点的聚类标签 # 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis') # 使用viridis色彩映射绘制结果图
plt.show() # 显示结果图 ```(三)OPTICS聚类
OPTICS(Ordering Points To Identify the Clustering Structure)是一种基于密度的聚类算法,它是为了优化DBSCAN算法而提出的。与DBSCAN类似,OPTICS算法的核心思想是通过分析样本点的密度分布来识别出数据集中的聚类结构。然而,OPTICS算法在处理过程中不直接产生聚类结果,而是生成一个有序的样本点列表,这个列表可以用来构建一个决策图,进而为DBSCAN算法选择合适的邻域半径参数。
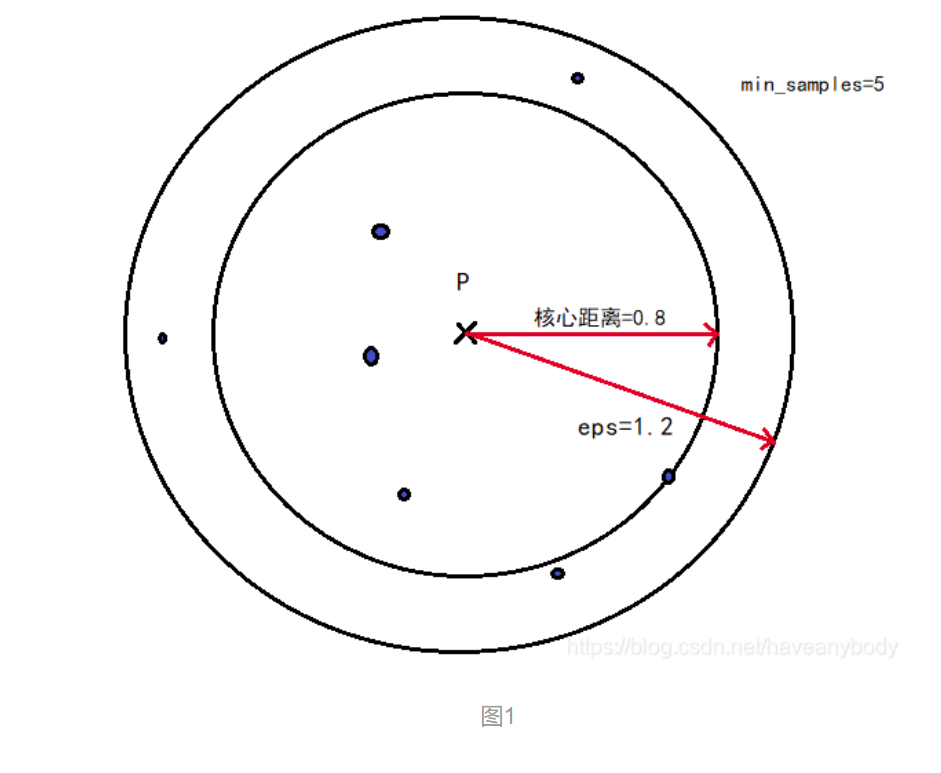
OPTICS算法引入了两个新的距离概念,即核心距离和可达距离:
核心距离:对于一个给定的核心对象X,使得X成为核心对象的最小邻域距离 r 就是X的核心距离。这句话乍一看有点绕,其实仔细读两遍就明白了,假如在DBSCAN中我们定义 eps = 1.2 和 min_samples=5,X在eps = 1.2的邻域内有8个样本点,则X是核心对象,但是我们发现距离X最近的第5个点和X的距离是0.8,那么核心对象 X 的核心距离就是 0.8,显然每个核心对象的核心距离并不都是相同的。参考图1,注意在计算 min_samples 的时候,一般也包括样本点自身,所以只需在P点eps邻域内找到7个点,那么P点就是核心点。
可达距离:如果X是核心对象,则对象 Y 到对象 X 的可达距离就是Y到X的欧氏距离和X的核心距离的最大值,如果X不是核心对象,则Y和X之间的可达距离就没有意义(不存在可达距离),显然,数据集中有多少核心对象,那么 Y 就有多少个可达距离。在下文介绍 API 的时候,我们会介绍在OPTICS中,一般默认设置 eps 为无穷大,即只要数据集的样本数不少于 min_samples,那么任意一个样本点都是核心对象,即都有核心距离,且任意两个对象之间都存在可达距离。
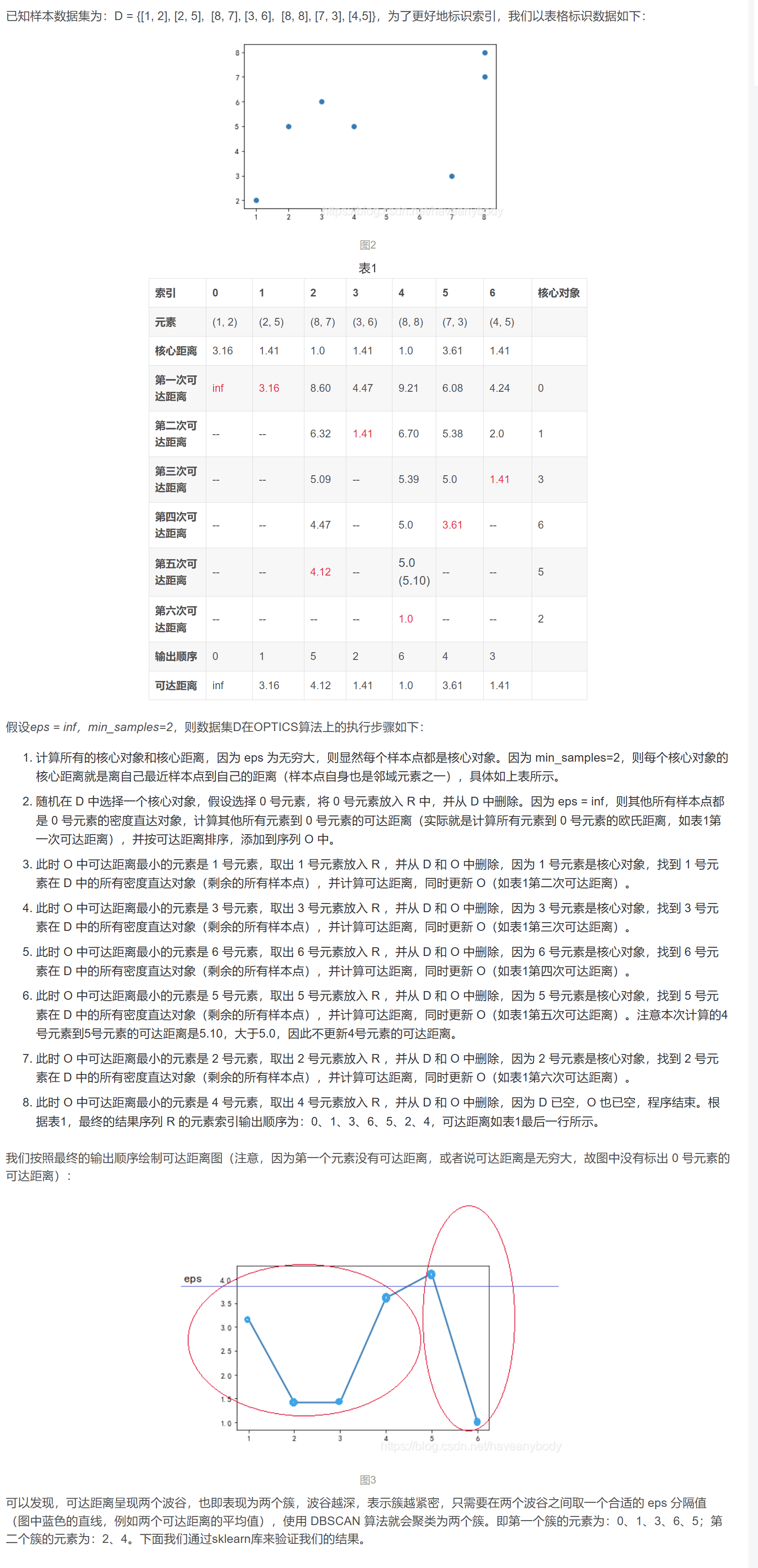
1、步骤
已知数据集 D,创建两个队列,有序队列O和结果队列R(有序队列用来存储核心对象及其该核心对象的密度直达对象,并按可达距离升序排列;结果队列用来存储样本点的输出次序。可以把有序队列里面放的理解为待处理的数据,而结果队列里放的是已经处理完的数据)。
如果D中所有点都处理完毕或者不存在核心点,则算法结束。否则,选择一个未处理(即不在结果队列R中)且为核心对象的样本点 p,首先将 p 放入结果队列R中,并从D中删除 p。然后找到 D 中 p 的所有密度直达样本点 x,计算 x 到 p 的可达距离,如果 x 不在有序队列 O 中,则将 x 以及可达距离放入 O 中,若 x 在 O 中,则如果 x 新的可达距离更小,则更新 x 的可达距离,最后对 O 中数据按可达距离从小到大重新排序。
如果有序队列 O 为空,则回到步骤2,否则取出 O 中第一个样本点 y(即可达距离最小的样本点),放入 R 中,并从 D 和 O 中删除 y。如果 y 不是核心对象,则重复步骤 3(即找 O 中剩余数据可达距离最小的样本点);如果 y 是核心对象,则找到 y 在 D 中的所有密度直达样本点,并计算到 y 的可达距离,然后按照步骤2将所有 y 的密度直达样本点更新到 O 中。
重复步骤2、3,直到算法结束。最终可以得到一个有序的输出结果,以及相应的可达距离。
通过上述流程,OPTICS算法最终会得到一个有序的输出结果和相应的可达距离。这个有序的结果可以用来绘制一个可达距离图,通过这个图可以观察到数据的聚类结构。
2、优缺点
- 无需预设聚类簇数,可发现不同密度和形状的簇。
- 对参数不敏感,鲁棒性强。
- 能自然发现噪声点和孤立点。
- 计算复杂度较高,训练大规模数据集时间较长。
- 聚类结构需结合可达距离图分析,理解与参数调整较为复杂。
3、使用场景
- 复杂、有噪声、密度不均的数据(如时序数据、地理数据、图像分割)。
- 无法预先确定簇数时的实际聚类分析。
4、代码
from sklearn.cluster import OPTICS
import numpy as np
# 定义样本数据集
X = np.array([[1, 2], [2, 5], [8, 7], [3, 6], [8, 8], [7, 3], [4, 5]])
# 执行OPTICS算法
clustering = OPTICS(min_samples=2).fit(X)
# 输出核心距离、样本点的排序、可达距离和聚类标签
print(clustering.core_distances_)
print(clustering.ordering_)
print(clustering.reachability_)
print(clustering.labels_)(四)K-Means 聚类模型
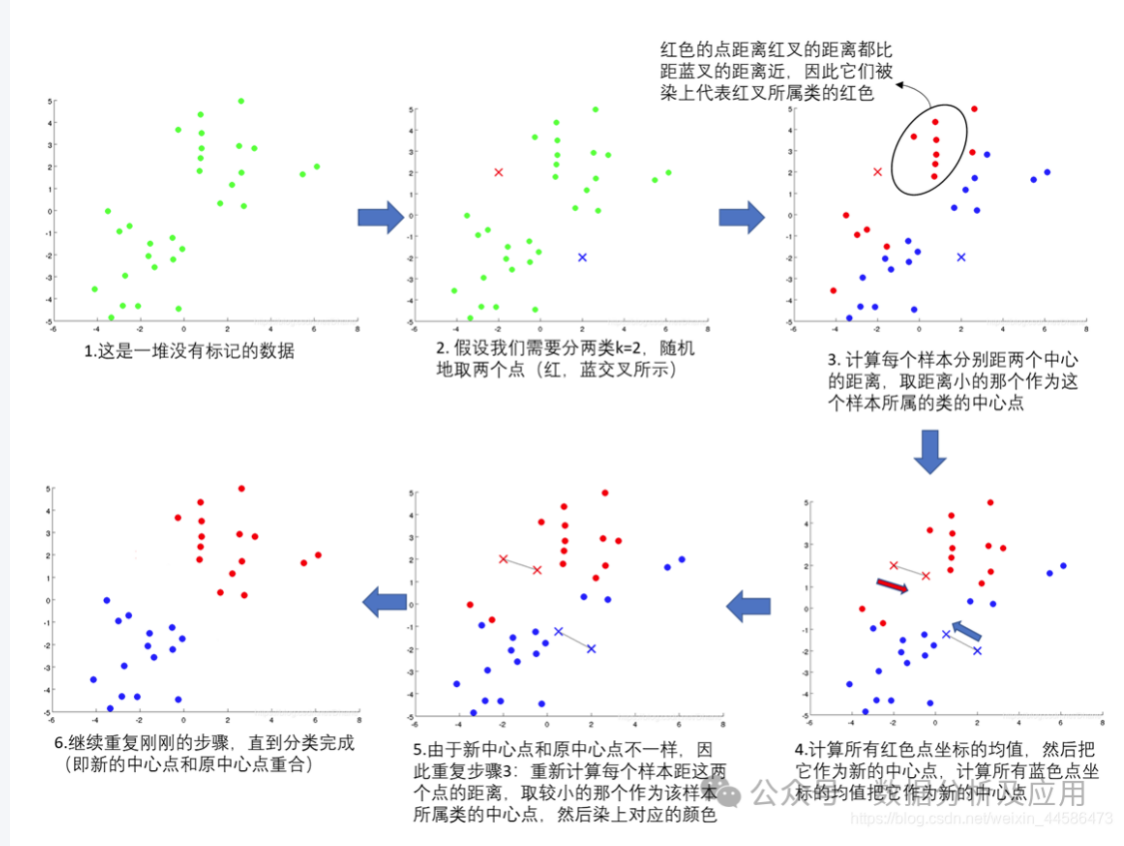
K-Means聚类是一种基于距离的聚类方法,通过最小化每个数据点到其所属簇中心点的距离之和,将数据点划分为K个簇。算法的主要思想是:每个簇有一个中心点,数据点被分配到最近的中心点所在的簇中。通过迭代更新每个簇的中心点,使得所有数据点到其所属簇的中心点的距离之和最小

1、步骤
- 初始化:随机选择K个中心点。
- 分配数据点:将每个数据点分配到最近的中心点所在的簇中。
- 更新中心点:重新计算每个簇的中心点,即簇中所有数据点的均值。
- 重复:重复步骤2和3,直到中心点不再发生显著变化或达到预设的迭代次数。
- 输出:返回K个簇的结果
2、优点
- 简单易理解:K-Means聚类模型简单直观,易于理解。
- 可扩展性:对于大规模数据集,K-Means算法具有较好的可扩展性。
- 无监督学习:K-Means是一种无监督学习方法,适用于未标记的数据集。
- 对异常值不敏感:由于是基于距离的聚类方法,异常值对聚类结果的影响较小。
- 参数敏感:对初始选择的K值和初始中心点敏感,不同的初始参数可能导致不同的聚类结果。
- 易陷入局部最优解:可能陷入局部最优解,而非全局最优解。
- 形状限制:只能发现球形簇,对于非球形簇的形状可能无法准确识别。
- 计算量大:对于高维数据,计算量较大。
3、使用场景
- 异常检测:K-Means聚类可以用于异常检测,将异常值识别为与其它数据点距离较远的簇。
- 市场细分:在市场营销领域,可以使用K-Means聚类将客户划分为不同的细分市场。
- 图像分割:在图像处理中,可以使用K-Means聚类进行图像分割,将图像划分为多个区域或对象。
- 特征提取:通过K-Means聚类可以提取数据的内在结构特征,用于分类或预测任务。
4、代码
from sklearn.cluster import KMeans # 导入K-Means聚类算法
from sklearn import datasets # 导入datasets用于生成样本数据
import matplotlib.pyplot as plt # 导入绘图库
iris = datasets.load_iris() # 使用Iris数据集作为示例
X = iris["data"] # 提取特征矩阵
kmeans = KMeans(n_clusters=3) # 假设有3个簇
labels = kmeans.fit_predict(X) # 获取每个样本点的聚类标签
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis') # 使用viridis色彩映射绘制结果图
plt.show() # 显示结果图 ```二、评价指标
常用评估指标包括外部评价指标和内部评价指标。外部评价指标是在已知真实标签的情况下评估聚类结果的准确性,而内部评价指标则是在不知道真实标签的情况下评估聚类结果的质量。
(一)外部指标

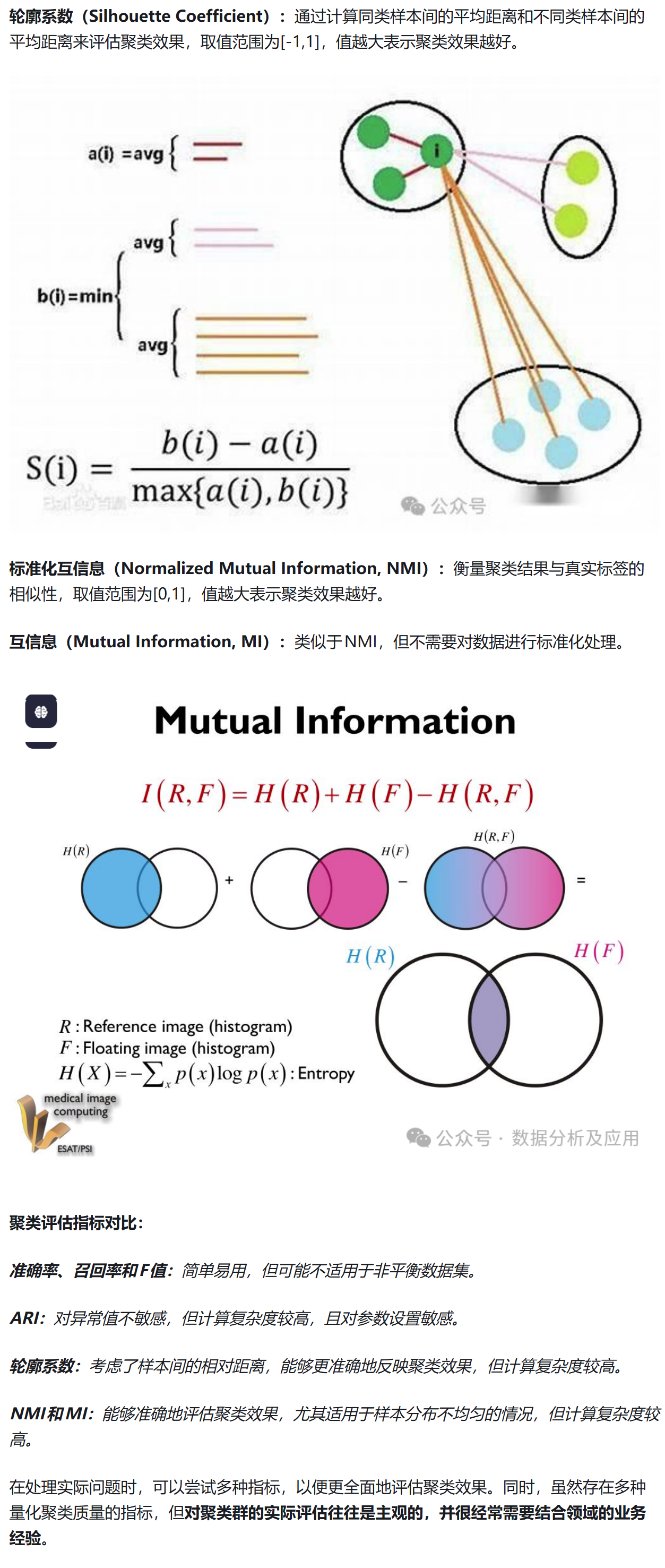
(二)内部指标

.jpg)

