栈和队列（持续更新中）

This article is mainly about my organization of the data structure. If you get any problems，you can ask me on GitHub.

1 栈

1.1 基本概念：

—栈是运算受限的线性表

—限制：插入和删除操作只能在同一端进行

—特点：后进先出(LIFO)或先进后出(FILO)

—栈是仅在表尾进行插入、删除操作的线性表。表尾称为栈顶(Top)，表头称为栈底(Base)。

1.2 数学内容

若n个元素顺序入栈，则可能的出栈顺序为C(2n,n)/(n+1)=(2n)!/((n+1)!n!)

1.3 顺序表示

==*加代码==

1.4 链式表示

//测试样例是PPT中十进制转八进制  1348
#include<stdio.h>
#include<stdlib.h>
#define ok 1
#define overflow 0
#define error 0
typedef int status;
typedef int selemtype;
typedef struct snode{
    selemtype date;
    struct snode *next;
}lsnode,*slnode;

status InitStack(slnode *h)//初始化 
{
    *h=(slnode)malloc(sizeof(lsnode));
    if(!*h) exit(overflow);
    (*h)->next=0;
    return ok; 
}

status Push(slnode *h,selemtype e)//入栈 
{
    slnode r;
    r=(slnode)malloc(sizeof(lsnode));
    if(!r) exit(overflow);
    r->date=e;
    r->next=(*h)->next;
    (*h)->next=r;
    return ok;    
}

status Pop(slnode *h,selemtype *e)//出栈 
{
    *h=(*h)->next;
    *e=(*h)->date;
    return ok;
}

status GetTop(slnode h, selemtype *e)//读栈顶 
{
    if(h->next==0) return error;
    *e=h->next->date;
    return ok; 
}

status StackEmpty(slnode h)//判断栈空 
{
    if(h->next==0) return 1;
    else return 0;
}

void fun1(selemtype n)
{
    printf("%d",n);
}

status StackTravers(slnode h, void (*fun1)(selemtype n))//遍历栈 
{
    slnode r=h->next;
    while(r!=0)
    {
        (*fun1)(r->date);
        r=r->next;
    }
    return ok;
}

status DestroyStack(slnode *h)//销毁栈 
{
    slnode r;
    while(*h)
    {
        r=*h;
        *h=(*h)->next;
        free(r);
    }
    free(*h); 
    return ok;
}

status StackLength(slnode h,int *i)//求栈长度 
{
    (*i)=0;
    slnode r=h->next;
    while(r)
    {
        (*i)++;
        r=r->next;
    }
    return ok;
 } 

int main()
{
    int m,i=0;
    scanf("%d",&m);
    slnode h;
    selemtype e;
    
    InitStack(&h);//初始化栈 
    printf("验证初始化栈：%d\n",h);
    DestroyStack(&h);//销毁栈  
    printf("验证毁灭栈：%d\n",h);
    
    InitStack(&h);//初始化栈 
    while(m!=0)//入栈 
    {
        Push(&h,m%8);
        m=m/8;
    }
    
    if(!StackEmpty(h))//判断栈空 
    {
        printf("遍历栈：") ;
        StackTravers(h,fun1);//遍历栈
        printf("\n"); 
    
        GetTop(h,&e);//读栈顶
        printf("读栈顶：%d\n",e); 
        
        StackLength(h,&i);//求栈长度 
        printf("求栈长：%d\n",i);    
     } 
    
    while(1)//出栈 
    {
        if(!StackEmpty(h))
        {
            Pop(&h,&e);
            printf("出栈：%d ",e);
                
            StackLength(h,&i);//求栈长度 
            printf("目前栈长：%d\n",i);
        }
        else break;
     } 
    
    DestroyStack(&h);//销毁栈
    return 0;
}

1.5 应用

1.5.1 数制转换

例题：设计算法，将十进制整数转换为八进制，在函数中输入数据并输出结果。

见链表表示

1.5.2 括号匹配

例题：假设通过键盘输入的一个表达式中只出现()和[]并允许任意顺序的嵌套，设计算法，检测括号是否匹配。

==*加代码==

1.5.3 迷宫求解

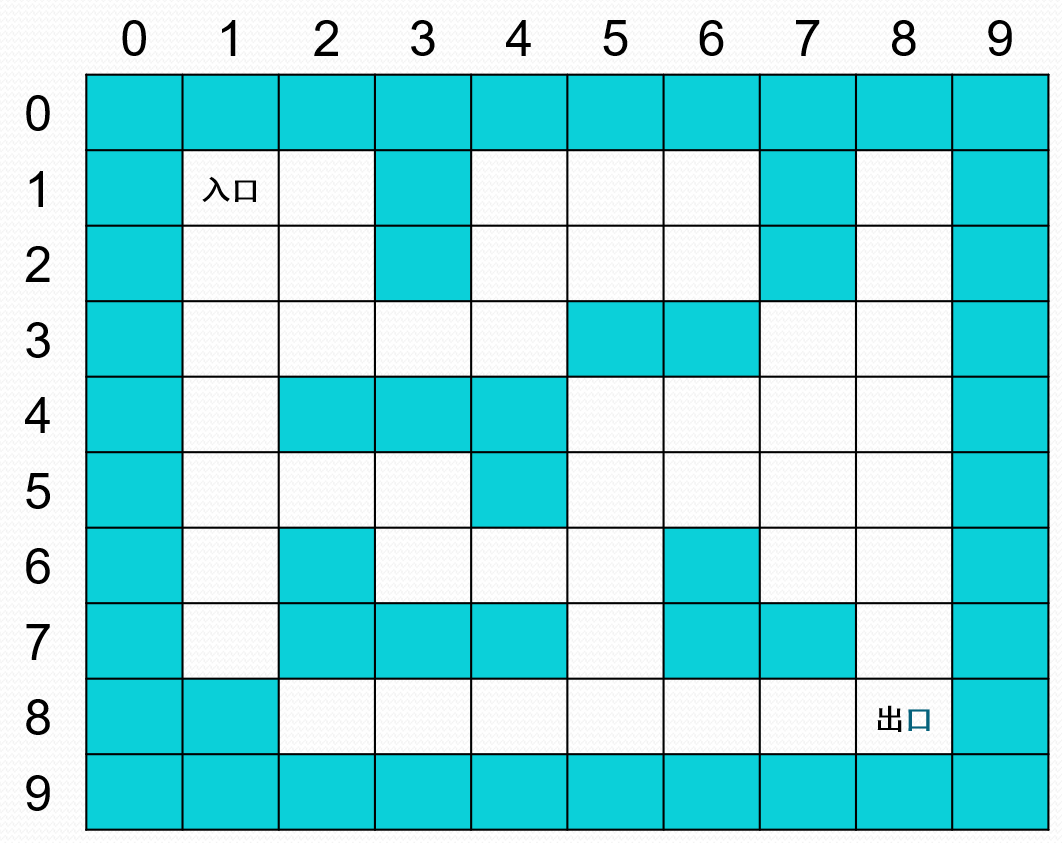
#include<stdio.h>
#include<stdlib.h>
#define ok 1
#define overflow 0
#define error 0
int maze[10][10]={
           {1,1,1,1,1,1,1,1,1,1},
           {1,0,0,1,0,0,0,1,0,1},
           {1,0,0,1,0,0,0,1,0,1},
           {1,0,0,0,0,1,1,0,0,1},
           {1,0,1,1,1,0,0,0,0,1},
           {1,0,0,0,1,0,0,0,0,1},
           {1,0,1,0,0,0,1,0,0,1},
           {1,0,1,1,1,0,1,1,0,1},
           {1,1,0,0,0,0,0,0,0,1},
           {1,1,1,1,1,1,1,1,1,1}};

typedef int status;
typedef struct{
    int x;
    int y;
}postype; 

typedef struct{
    int di;
    int step;
    postype    seat; 
}selemtype;



typedef struct snode{
    selemtype date;
    struct snode *next;
}lsnode,*slnode;

status InitStack(slnode *h)//初始化 
{
    *h=(slnode)malloc(sizeof(lsnode));
    if(!*h) exit(overflow);
    (*h)->next=0;
    return ok; 
}

status Push(slnode *h,selemtype e)//入栈 
{
    slnode r;
    r=(slnode)malloc(sizeof(lsnode));
    if(!r) exit(overflow);
    r->date=e;
    r->next=(*h)->next;
    (*h)->next=r;
    return ok;    
}

status Pop(slnode *h,selemtype *e)//出栈 
{
    *h=(*h)->next;
    *e=(*h)->date;
    return ok;
}

status GetTop(slnode h, selemtype *e)//读栈顶 
{
    if(h->next==0) return error;
    *e=h->next->date;
    return ok; 
}

status StackEmpty(slnode h)//判断栈空 
{
    if(h->next==0) return 1;
    else return 0;
}

void fun1(selemtype n)
{
    printf("%d",n);
}

status StackTravers(slnode h, void (*fun1)(selemtype n))//遍历栈 
{
    slnode r=h->next;
    while(r!=0)
    {
        (*fun1)(r->date);
        r=r->next;
    }
    return ok;
}

status DestroyStack(slnode *h)//销毁栈 
{
    slnode r;
    while(*h)
    {
        r=*h;
        *h=(*h)->next;
        free(r);
    }
    free(*h); 
    return ok;
}

status StackLength(slnode h,int *i)//求栈长度 
{
    (*i)=0;
    slnode r=h->next;
    while(r)
    {
        (*i)++;
        r=r->next;
    }
    return ok;
 } 

status pass(postype pos)
{
    if(maze[pos.x][pos.y]==0) return 1;
    else return 0;
 } 
 
postype nextpos(postype pos,int di)
 {
     switch(di)
     {
         case 1:pos.x++;break;
         case 2:pos.y++;break;
         case 3:pos.x--;break;
        case 4:pos.y--;break;
     }
     return pos;
 }
 

status mazepath(int maze[10][10],postype start,postype end)
{
    slnode h;
    InitStack(&h);//初始化栈
    selemtype e;
    postype curpos=start;
    int curstep=1;
    do
    {
        if(pass(curpos))
        {
            maze[curpos.x][curpos.y]=curstep;
            e.step=curstep;
            e.di=1;
            e.seat=curpos;
            Push(&h,e);
            if(curpos.x==end.x&&curpos.y==end.y) return 1;
            curpos=nextpos(curpos,1);
            curstep++;
        }
        else
        {
            if(!StackEmpty(h)) 
            {
                Pop(&h,&e);
                while(e.di==4&&!StackEmpty(h))
                {
                    maze[e.seat.x][e.seat.y]=-1;
                    Pop(&h,&e);
                }
                
                if(e.di<4)
                {
                    e.di++;
                    Push(&h,e);
                    curpos=nextpos(e.seat,e.di);
                }
            }
        }
    
    }while(!StackEmpty(h));
    return error;
}

int main()
{
    int i,j;
    postype start={1,1},end={8,8};
     for(i=0;i<10;i++)
   {
     for(j=0;j<10;j++)
       printf("%3d",maze[i][j]);
     printf("\n");
   }
   printf("\n");
   
   if(!mazepath(maze,start,end))
       printf("无解！\n");
       
   for(i=0;i<10;i++)
   {
     for(j=0;j<10;j++)
       printf("%3d",maze[i][j]);
     printf("\n");
   }
    return 0;    
}

2 队列

2.1 基本概念：

—队列是运算受限的线性表

—限制：一端插入，另一端删除

—特点：先进先出(FIFO)

—允许插入(入队)的一端称队尾、允许删除(出队)的一端称队头。

2.2 顺序表示

==*加代码==

2.3 链式表示

==*加代码==

2.4 应用——离散事件模拟

假设某银行有N个窗口对外接待客户，从银行开门起不断有客户进入银行，若有窗口空闲，则直接办理业务，反之，则排在人数最少的窗口后面。编写一个程序来模拟银行业务并计算客户在银行逗留的平均时间。

思路：1. 0分钟：银行开门，假定一客户到达。只要有客户到达，就产生两个随机数，分别表示该客户的业务办理时间和下一客户到达的时间间隔(例如随机数为8和5)，并排在人数最少的队列中。2. 此时可确定，5分钟后将有一个客户到达事件发生，8分钟时将有一个客户离开事件发生。3. 5分钟：客户到达，产生两个随机数(例如25和4)，该客户何时离开？若排在空窗口，30分钟时，否则当他为队头时计算。

事件链表：客户到达事件(0)和客户离开事件(i)，按事件发生时间非递减有序；窗口队列：模拟排队效果，记录客户到达时间和业务办理时间

==*加代码==

3 习题

例题1：

假设一个栈的输入序列为1,2,3，若在入栈的过程中允许出栈，则可能得到的出栈序列是什么？

① 1入1出， 2入2出，3入3出， 即123；

② 1入1出， 2、3入，3、2出， 即132；

③ 1、2入，2出， 3入3出， 即231；

④ 1、2入，2、1出，3入3出， 即213；

⑤ 1、2、3入，3、2、1出， 即321；

例题2：

假设一个栈的输入序列是12345，若在入栈的过程中允许出栈，则栈的输出序列12345可能实现吗？ 43512的输出呢？

12345 可能；43512 不可能

4 附录——ADT定义

1.栈

ADT Stack {
数据对象：D＝{ ai | ai ∈ElemSet, i=1,2,...,n, n≥0 }
数据关系：R1＝{ <ai-1, ai >| ai-1, ai∈D, i=2,...,n }
                      约定an 端为栈顶，a1 端为栈底。
基本操作：
InitStack(&S)
    操作结果：构造一个空栈S
DestroyStack(&S)
    初始条件：栈 S 已存在。
    操作结果：栈 S 被销毁。
ClearStack(&S)
    初始条件：栈 S 已存在。
    操作结果：将 S 清为空栈。
StackEmpty(s)
    初始条件：栈 S 已存在。
    操作结果：若栈 S 为空栈，返回 TRUE，否则返回 FALSE。
StackLength(S)
    初始条件：栈 S 已存在。
    操作结果：返回 S 的元素个数，即栈的长度
GetTop(S, &e)
    初始条件：栈 S 已存在且非空。
    操作结果：用 e 返回 S 的栈顶元素。
Push(&S, e)
    初始条件：栈 S 已存在。
    操作结果：插入元素 e 为新的栈顶元素。
Pop(&S, &e)
    初始条件：栈 S 已存在且非空。
    操作结果：删除栈顶元素，并用 e 返回其值。
StackTravers(S, visit())
    初始条件：栈 S 已存在且非空。
    操作结果：从栈底开始遍历栈。
} ADT Stack

2.队列

ADT Queue {
数据对象：D＝{ ai | ai ∈ElemSet, i=1,2,...,n, n≥0 }
数据关系：R1＝{ <ai-1, ai >| ai-1, ai∈D, i=2,...,n }
                      约定an 端为队尾，a1 端为队头。
基本操作：
InitQueue(&Q)
    操作结果：构造一个空队列Q。
DestroyQueue(&Q)
    初始条件：队列Q已存在。
    操作结果：队列Q被销毁， 不再存在。
ClearQueue(&Q)
    初始条件：队列Q已存在。
    操作结果：将Q清为空队列。
QueueEmpty(Q)
    初始条件：队列Q已存在。
    操作结果：若Q为空队列，则返回TRUE，否则返回FALSE。
QueueLength(Q)
    初始条件：队列Q已存在。
    操作结果：返回Q的元素个数，即队列的长度
GetHead(Q, &e)
    初始条件：Q为非空队列。
    操作结果：用e返回Q的队头元素。
EnQueue(&Q, e)
    初始条件：队列Q已存在。
    操作结果：插入元素e为Q的新的队尾元素。
DeQueue(&Q, &e)
    初始条件：Q为非空队列。
    操作结果：删除Q的队头元素，并用e返回其值
}ADT Queue