This article is mainly about my organization of the data structure. If you get any problems,you can ask me on GitHub.
1 二叉树
1.1 二叉树的数学内容
1.1.1 性质
性质1: 在二叉树的第i层上至多有 $ _2 i$ -1个结点(i>=1)。
性质2:深度为k的二叉树至多有$ _2 k-1 $个结点(k>=1)
性质3: 对任何一棵二叉树,如果其终端结点数为n0,度为2的结点数为n2,则 n0=n2+1。
完全二叉树的性质:
性质4 :具有 n 个结点的完全二叉树的深度为 $ \log_{2} n+1$
性质5: 如果对一棵有n个结点的完全二叉树的所有结点按层序编号(自上向下,同层从左到右),则对任一结点i (1<=i<=n),有:
(1)如果i=1,则结点i无双亲,是二叉树的根;如果i>1,则其双亲是结点 i/2向下取余。
(2)如果2i>n,则结点i为叶子结点,无左孩子;否则,其左孩子是结点2i。
(3)如果2i+1>n,则结点i无右孩子;否则,其右孩子是结点2i+1。
1.1.2 三个推论
推论1:具有n个结点的二叉树可能的形态数为C(2n,n)
推论2:完全二叉树中1度结点的个数为0或1
推论3:具有n个结点的二叉树,其二叉链表中空指针域的个数为n+1
1.1.3 两个定理
定理1:n(n>=0)个结点的二叉树,均可由它的中序序列和先序序列唯一确定。
定理2:n(n>=0)个结点的二叉树,均可由它的中序序列和后序序列唯一确定。
1.2 二叉树的存储结构
1.2.1 顺序存储
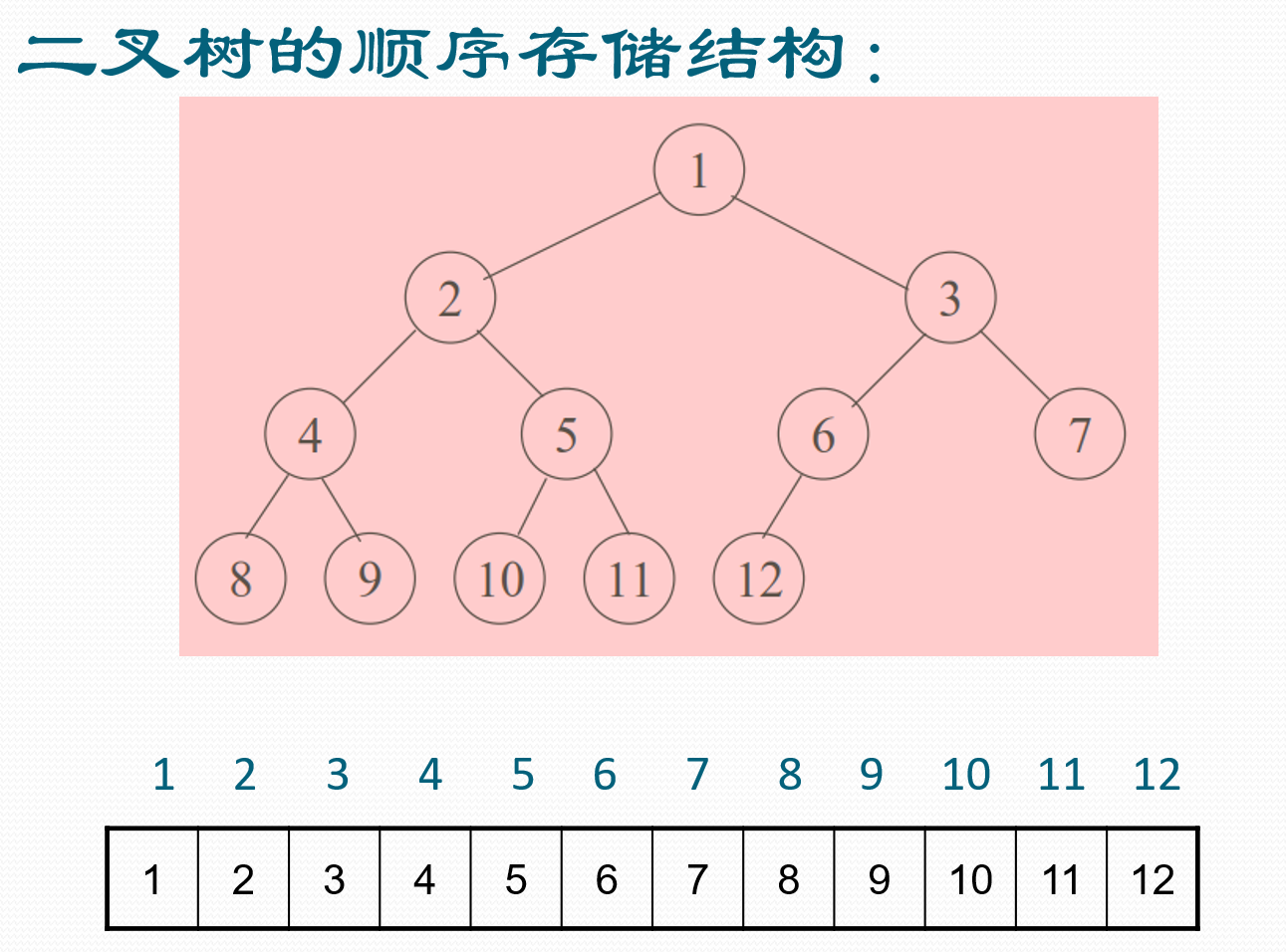
只适用于完全二叉树,根据性质5可以判断双亲和孩子
==建立顺序表*加代码==
1.2.2 链式存储(前2种重点)
1.2.2.1 二叉链表
直观的表示出了某结点左右孩子的信息
==建立二叉链表*加代码==
先根遍历
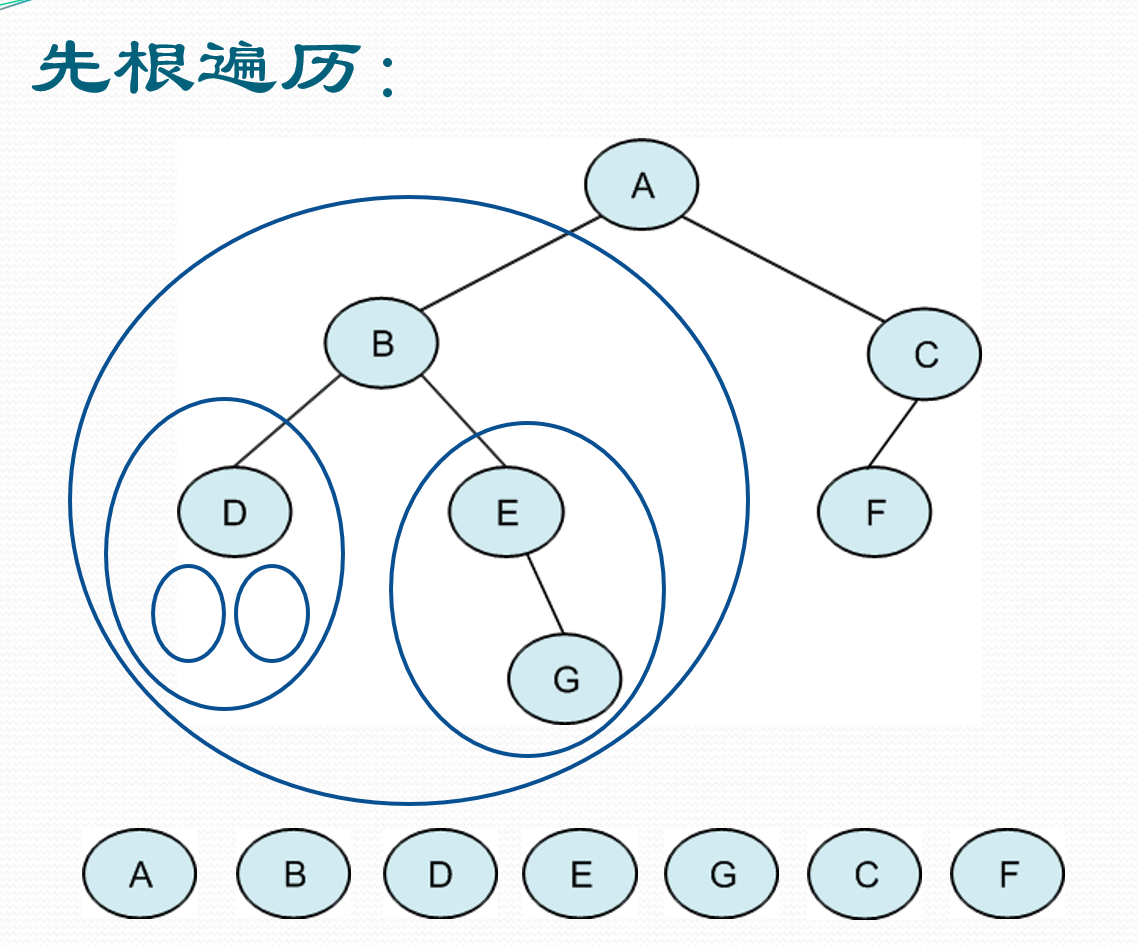
递归算法
==*加代码==
非递归算法
==*加代码==
中根遍历
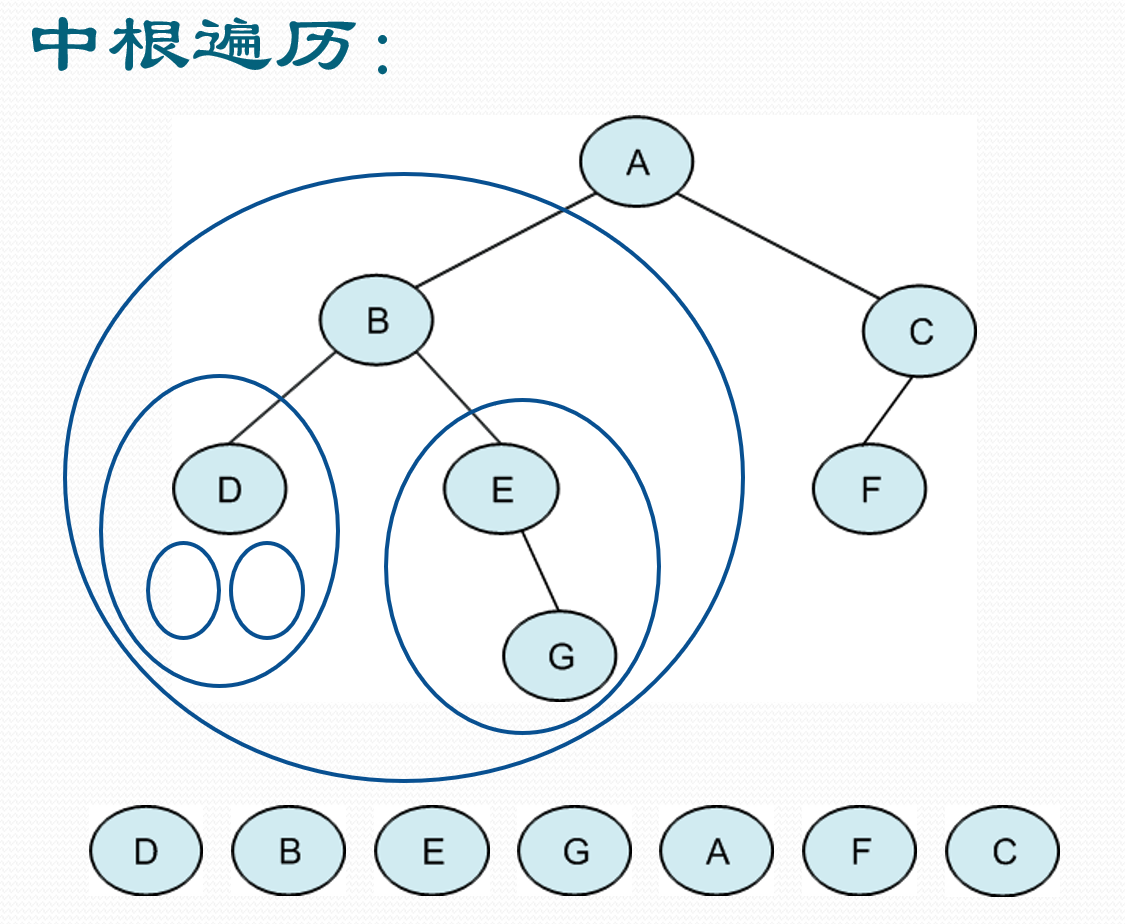
后根遍历
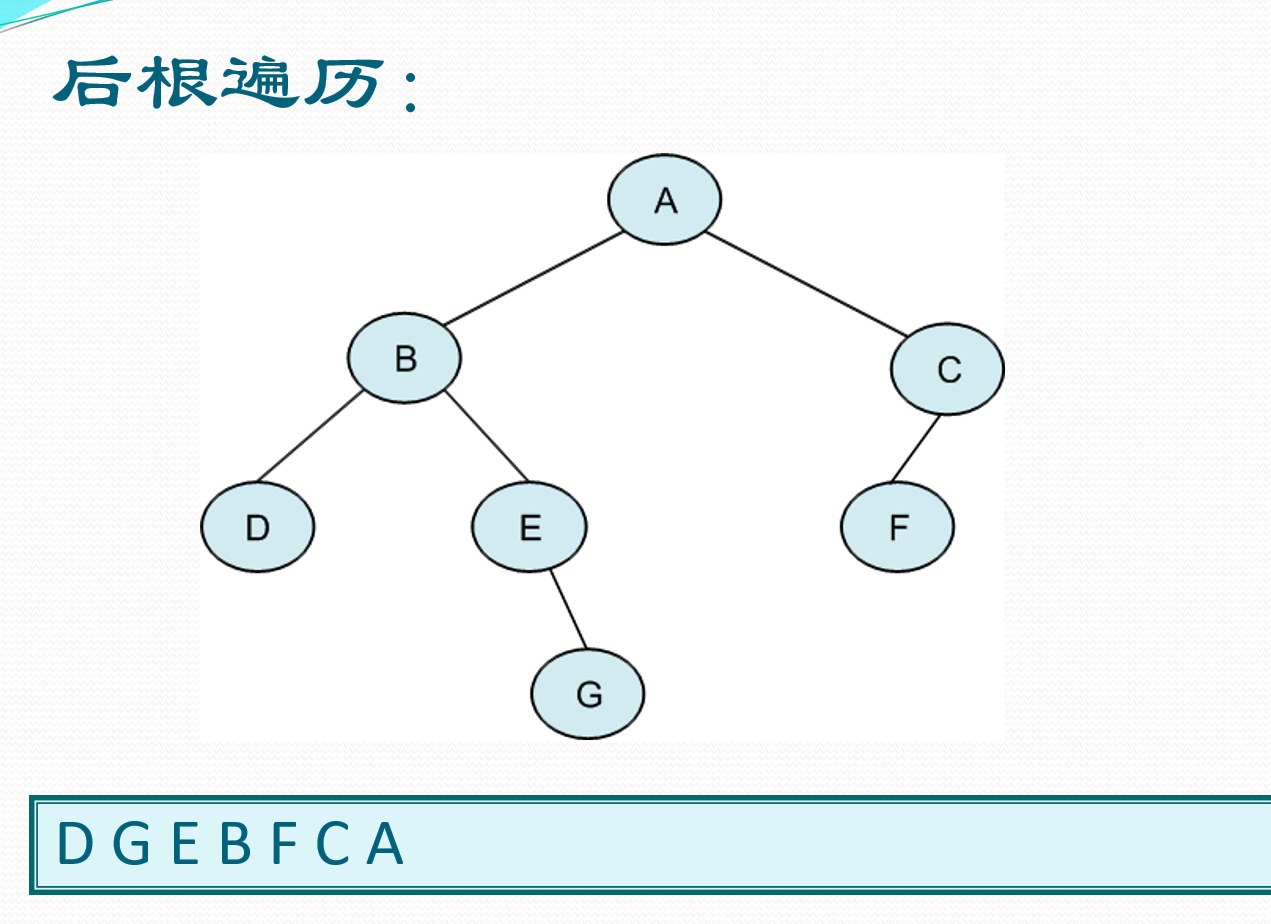
1.2.2.2 线索链表
为了直观的表示出某结点的前驱和后继
先序线索化
==*加代码==
中序线索化
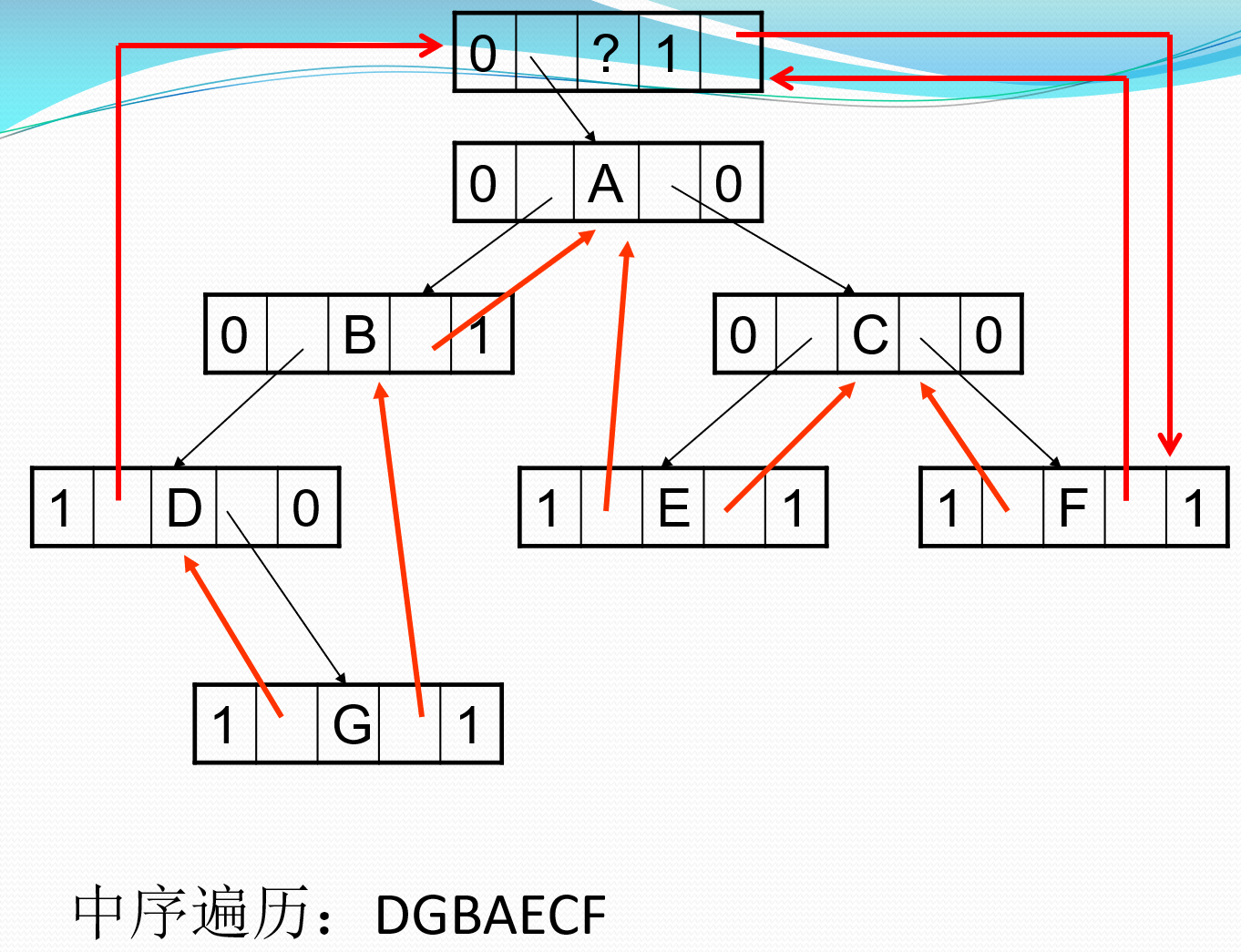
==*加代码==
后序线索化
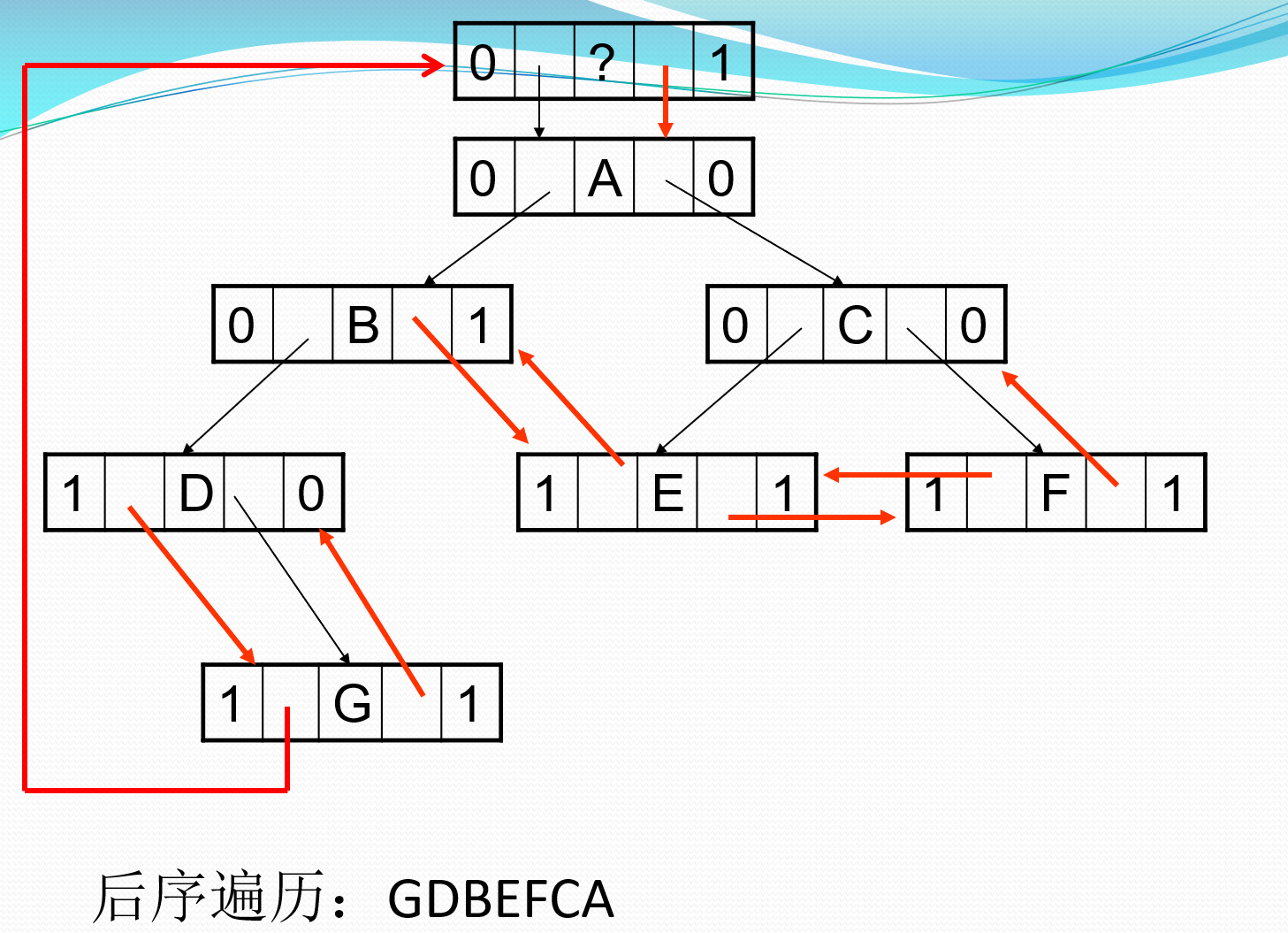
==*加代码==
1.2.2.3 三叉链表
1.2.2.4 双亲链表
2 树和森林
2.1 树的存储结构
2.1.1 双亲表示法
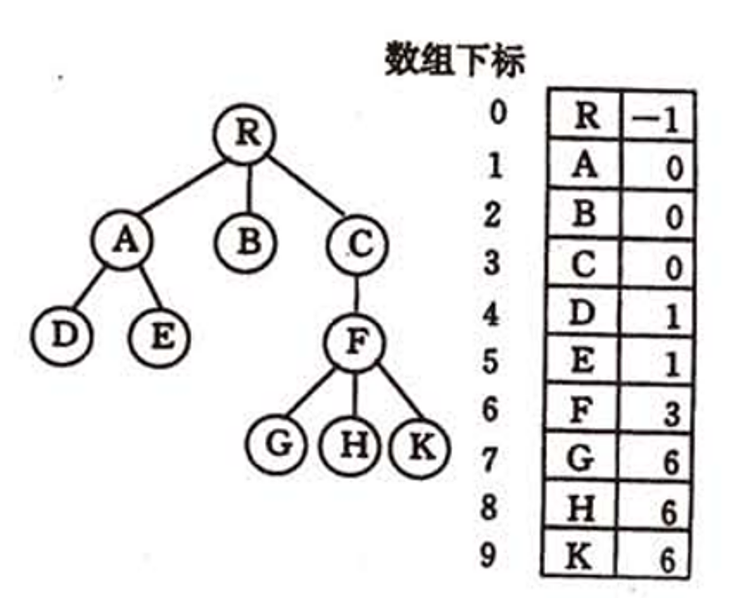
==*加代码==
2.1.2 孩子表示法
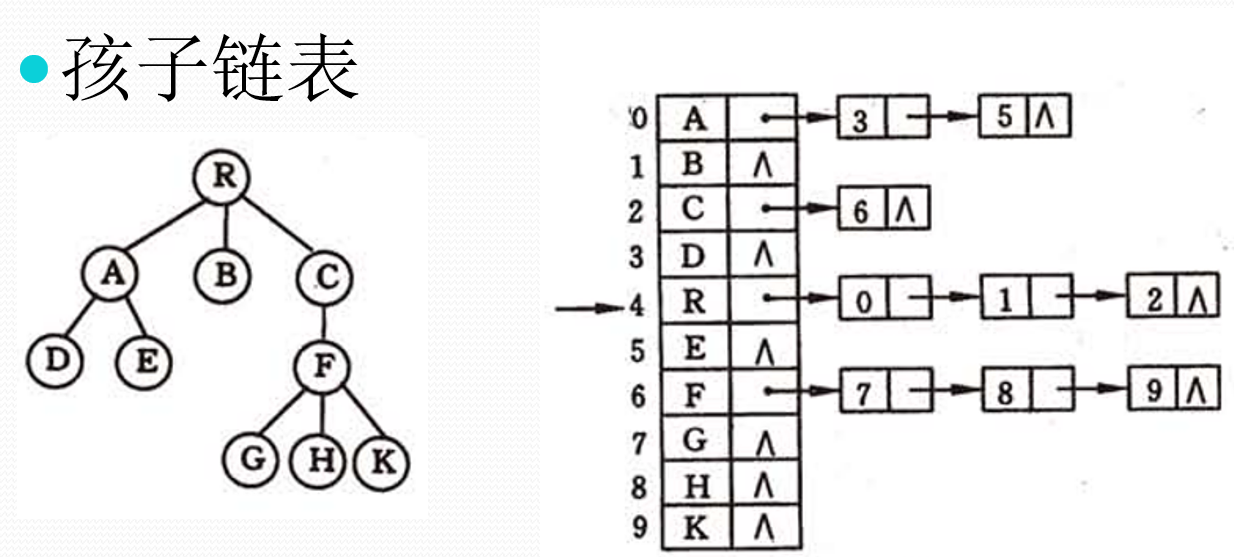
==*加代码==
2.1.3 孩子兄弟表示法
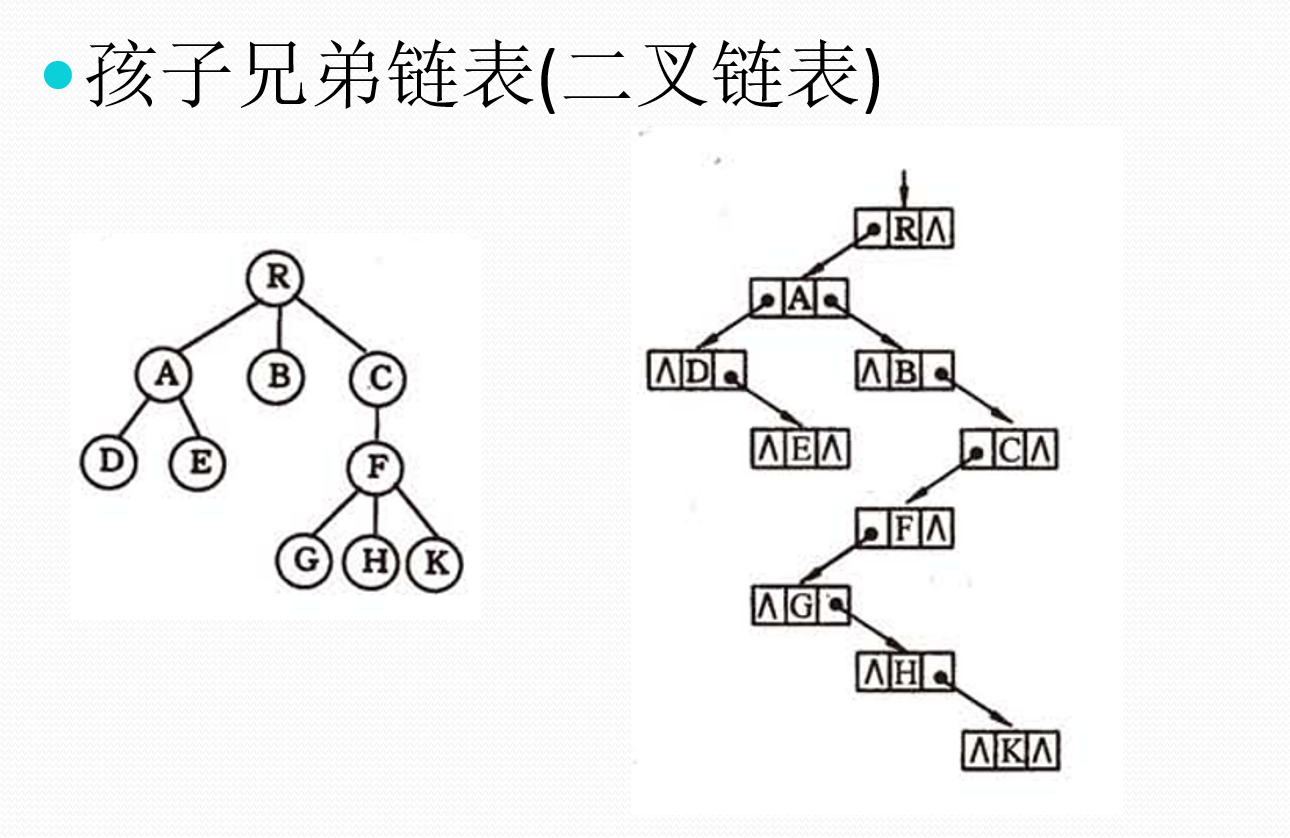
==*加代码==
2.2 树和二叉树的转换
树和二叉树均可以使用二叉链表为存储结构,则通过二叉链表作为媒介,树和二叉树可以相互转换
第一步:加线:在兄弟之间加一连线
第二步:抹线:对每个结点,除了其左孩子外,去除其与其余孩子之间的关系
第三步:旋转:横线顺时针旋转45°
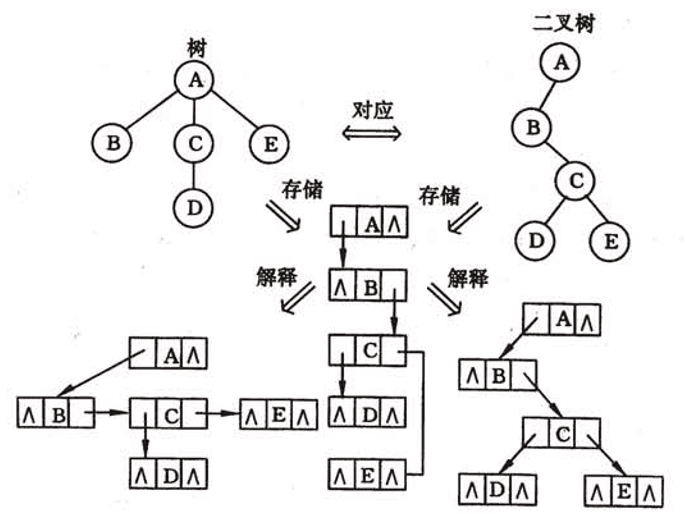
==*加代码==
2.3 森林和二叉树
树转换为二叉树后,右子树必为空。
将森林中的每棵树依次转换为二叉树,并将第i棵二叉树的根作为第i-1棵二叉树根的右孩子(2<=i<=m)。
如果F={T1,T2,…,Tm}是森林,则可按如下规则转换成一棵二叉树B=(root,LB,RB)
1.若F为空,则B为空树
2.若F非空,则B的根root即为森林中第一棵树的根ROOT(T1);B的左子树LB是从T1中根结点的子树森林F1={T11,T12,…,T1m1}转换而成的二叉树;其右子树RB是从森林F’={T2,T3,…,Tm}转换而成的二叉树
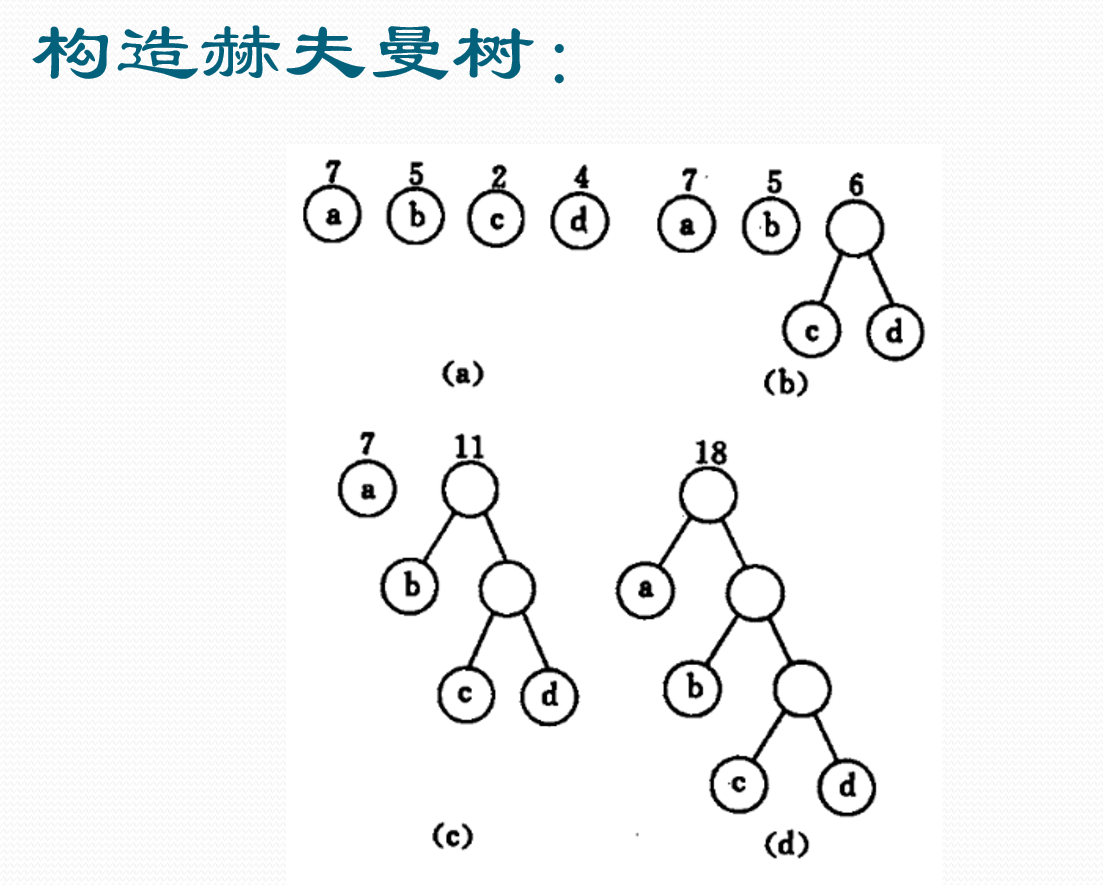
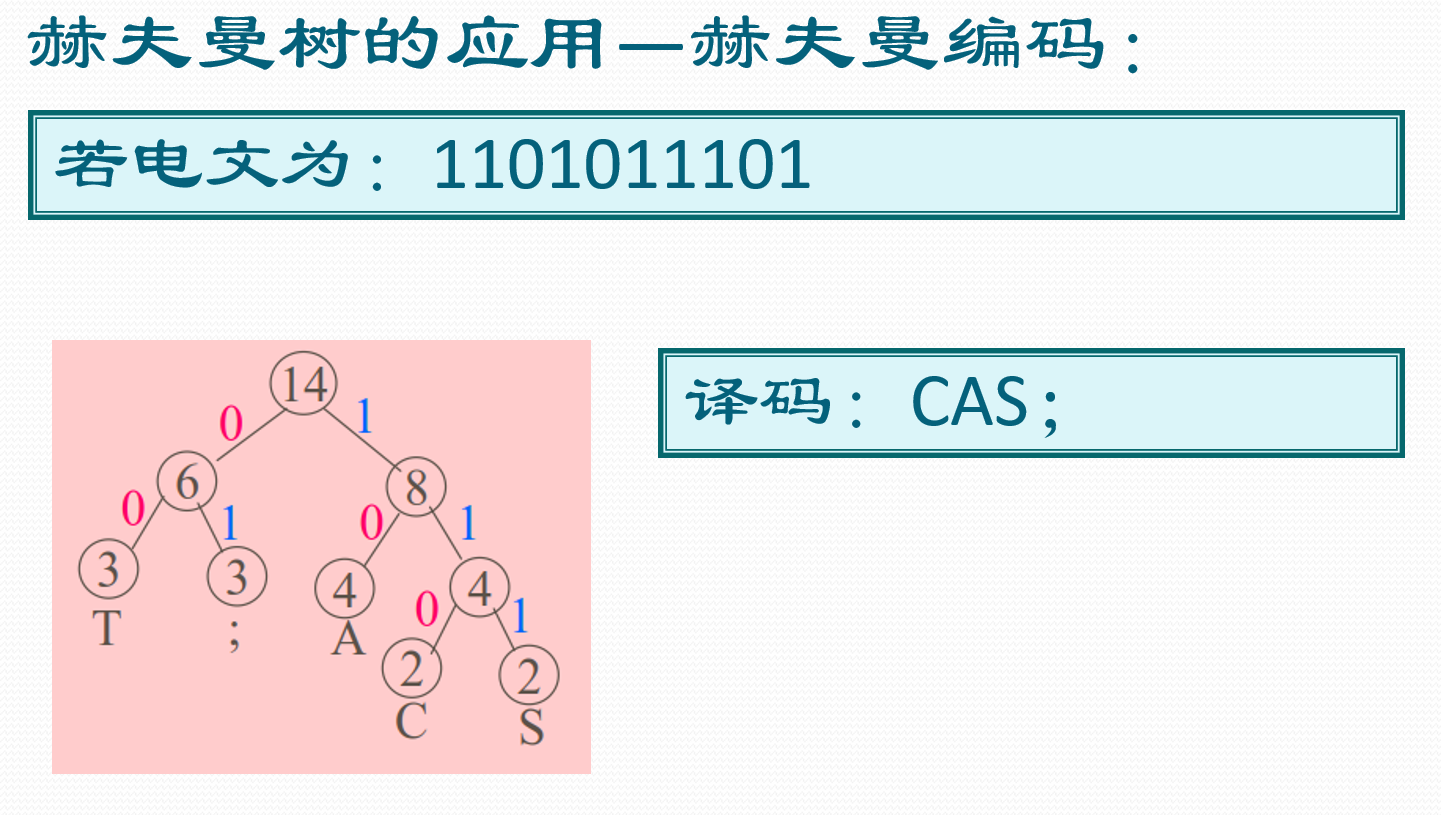
2.4 赫夫曼树
带权路径长度最短的树(最优二叉树)
树的路径长度:从树根到每一个结点的路径长度之和
结点的带权路径长度:带权结点(叶子)到根的路径长度与权的乘积
树的带权路径长度:树中所有结点的带权路径长度之和
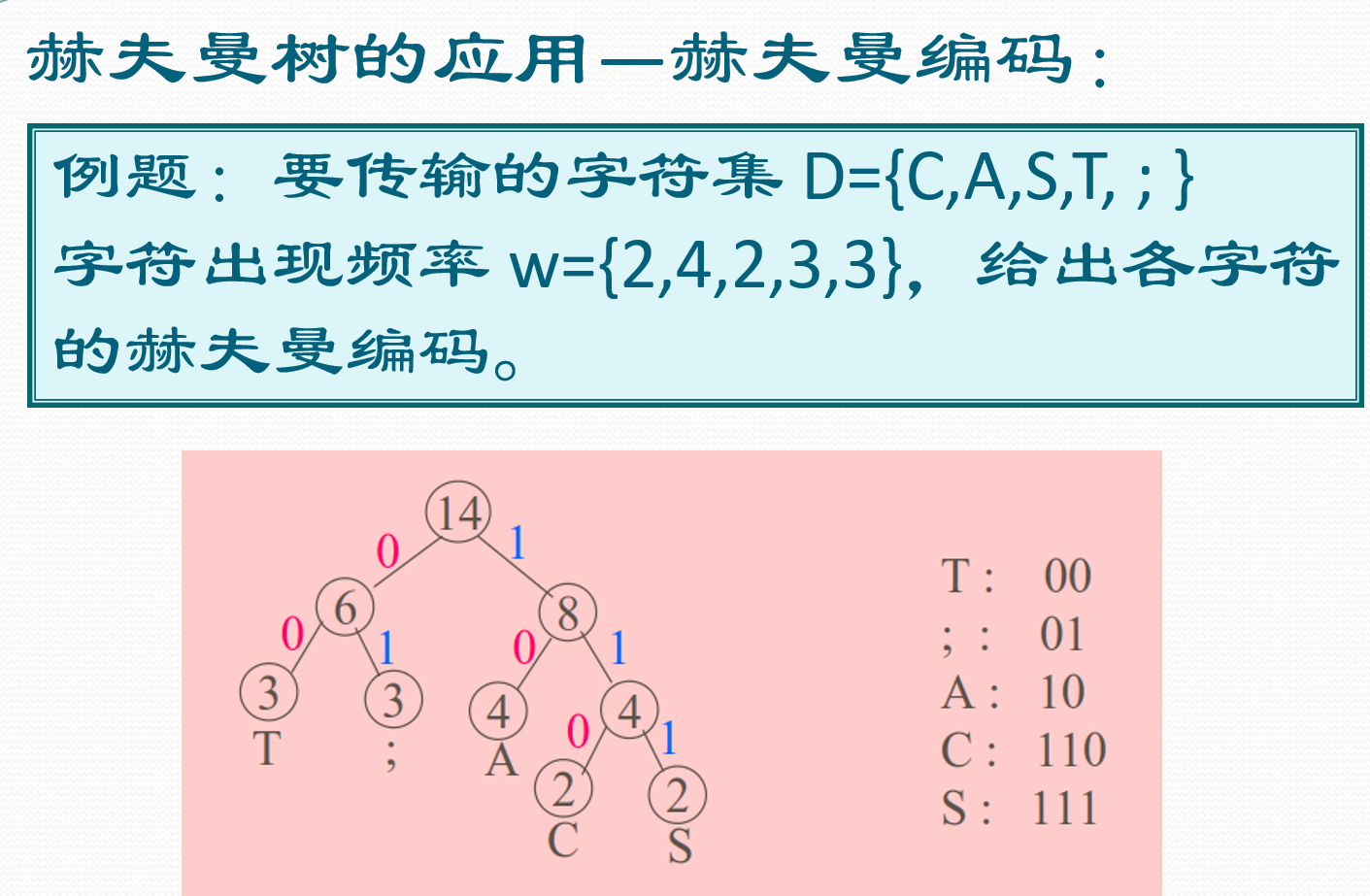
赫夫曼树的应用——赫夫曼编码
3 习题
例题1:
假设一棵完全二叉树有700个结点,则其叶子结点有多少个?
根据性质4,700个结点的完全二叉树为10层
根据性质2,前9层有511个结点,则第10层结点数为189个,均为叶子结点
根据性质1,第9层结点数为256个,其中前95个为第10层189个结点的双亲,因此第9层的叶子数为161个
所以叶子结点总数为189+161=350个
例题2:
1.若二叉树T,先序遍历序列为ABCDEF ,中序遍历序列为CBAEDF ,则其后序遍历序列为?
C B E F D A
2.已知二叉树的先序序列为ABDEGCF,中序序列为DBGEACF,则后序序列为( )
要点:先序或后序确定根;中序确定左右子树
例题3:
1.某二叉树的先序遍历和后序遍历的序列正好相反,则该二叉树一定是( )
A 空树或只有一个结点 B 完全二叉树
C 二叉排序树 D 高度与结点数相同
要点:先序:根左右;后序:左右根
2.一棵二叉树的先序遍历序列为abcdefg,它的中序遍历序列可能是( )
A cabdefg B abcdefg
C dacefbg D adcbgef
要点:先序:根左右;中序:左根右
3.如果二叉树结点的先序序列、中序序列和后序序列中,结点A、B的位置都是A在前B在后,则A B可能是兄弟么?A可能是B的双亲么?A可能是B的孩子么?
要点:先序:根左右;中序:左根右;后序:左右根
4.一棵二叉树的先序、中序和后序序列分别如下,其中一部分未显示出来。试求出空格处的内容,并画出该树
先序:()B()F()I C E H() G
中序: D()K F I A()E J C ()
后序:()K()F B H J ()G()A
例题4:
==*加代码==
1.假设二叉树采用二叉链表存储结构,设计一个算法,求前序遍历序列中第K个结点的结点值。
2.假设二叉树采用二叉链表存储结构,设计一个算法,按层次遍历二叉树
3.假设二叉树采用二叉链表存储结构,设计一个算法,求二叉树T的宽度(即结点数最多的层次上的结点个数)。
4.假设二叉树采用二叉链表存储结构,设计一个算法,判断一棵二叉树是否为完全二叉树。
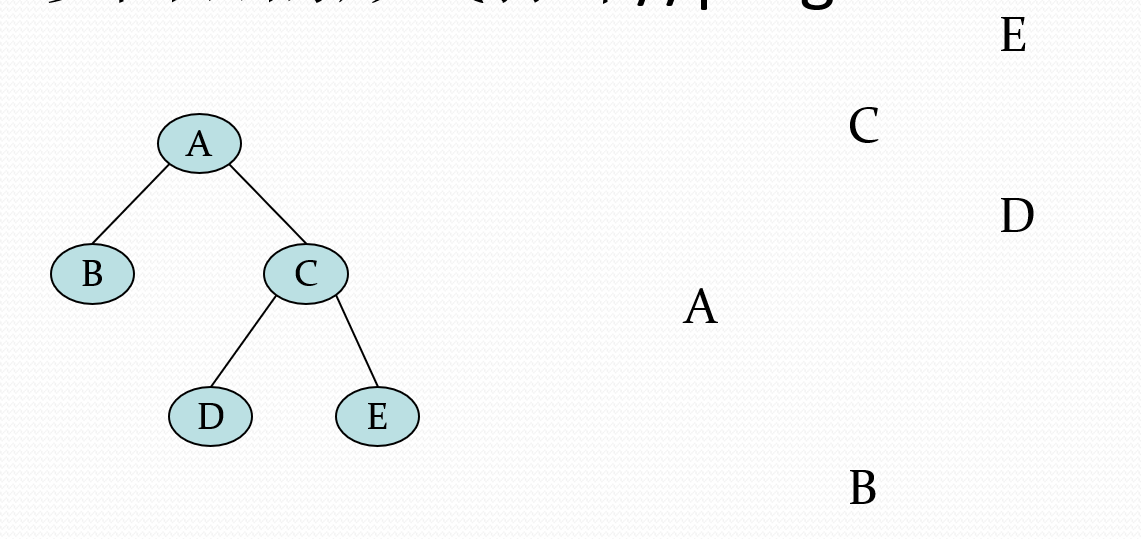
5.设计一个递归算法,将一棵二叉树逆时针90度打印出来。如下图左的二叉树,以图右的形式打印
6.设计在一棵中序线索二叉树中查找中序序列的最后一个结点和任一结点中序前驱结点的算法,并在此基础上设计非递归的中序反向遍历算法。
例题5:
1.引入线索二叉树的目的是( )
A 加快查找前驱和后继的速度
B 为了在二叉树中方便的插入和删除
C 为了方便的找到双亲
D 使二叉树的遍历结果唯一
2.判断线索二叉树中*p结点有右孩子的条件是
P->rtag==0
3.在n个结点的线索二叉树上含有的线索数为
n+1
例题6:
1.给出在先序线索二叉树中查找*p的后继结点的过程。
2.先序线索中,若*p的左孩子不空,则左孩子为后继;否则其后继为右孩子或右线索。
3.给出在后序线索二叉树中查找*p的后继结点的过程。
4.在后序线索中,若*p有右线索,则右线索为其后继;否则,其后继为其双亲结点右子树后序序列中的第一个结点,若双亲无右子树,则后继即为双亲。
4 附录——ADT定义
1.二叉树
ADT BinaryTree{
数据对象: D={ai|ai∈ElemSet,i=1,2,...,n, n≥0 }
数据关系: R
基本操作:
InitBiTree(&T);
DestroyBiTree(&T);
CreateBiTree(&T, definition);
ClearBiTree(&T);
BiTreeEmpty(T);
BiTreeDepth(T);
Assign(T, &e, value);
Root(T);
Value(T, e);
Parent (T, e);
LeftChild (T, e);
RightChild (T, e);
LeftSibling (T, e);
RightSibling (T, e);
PreOrderTraverse(T, Visit());
InOrderTraverse(T, Visit());
PostOrderTraverse(T, Visit());
LevelOrderTraverse(T, Visit());
InsertChild(T, p, LR, c);
DeleteChild(T, p, LR);
} ADT BinaryTree

