递归问题算法（持续更新中）

This article is mainly about my organization of the data structure. If you get any problems，you can ask me on GitHub.

1 n!

double fun(int n){
    double x;
    if(n==0) x=1;
    else  x=n* fun(n-1);
    return  x;
}

2 斐波那契数列第n项的值

long  fun(int n){
    if(n==1||n==2) return 1;
    else return fun(n-1)+fun(n-2);
}

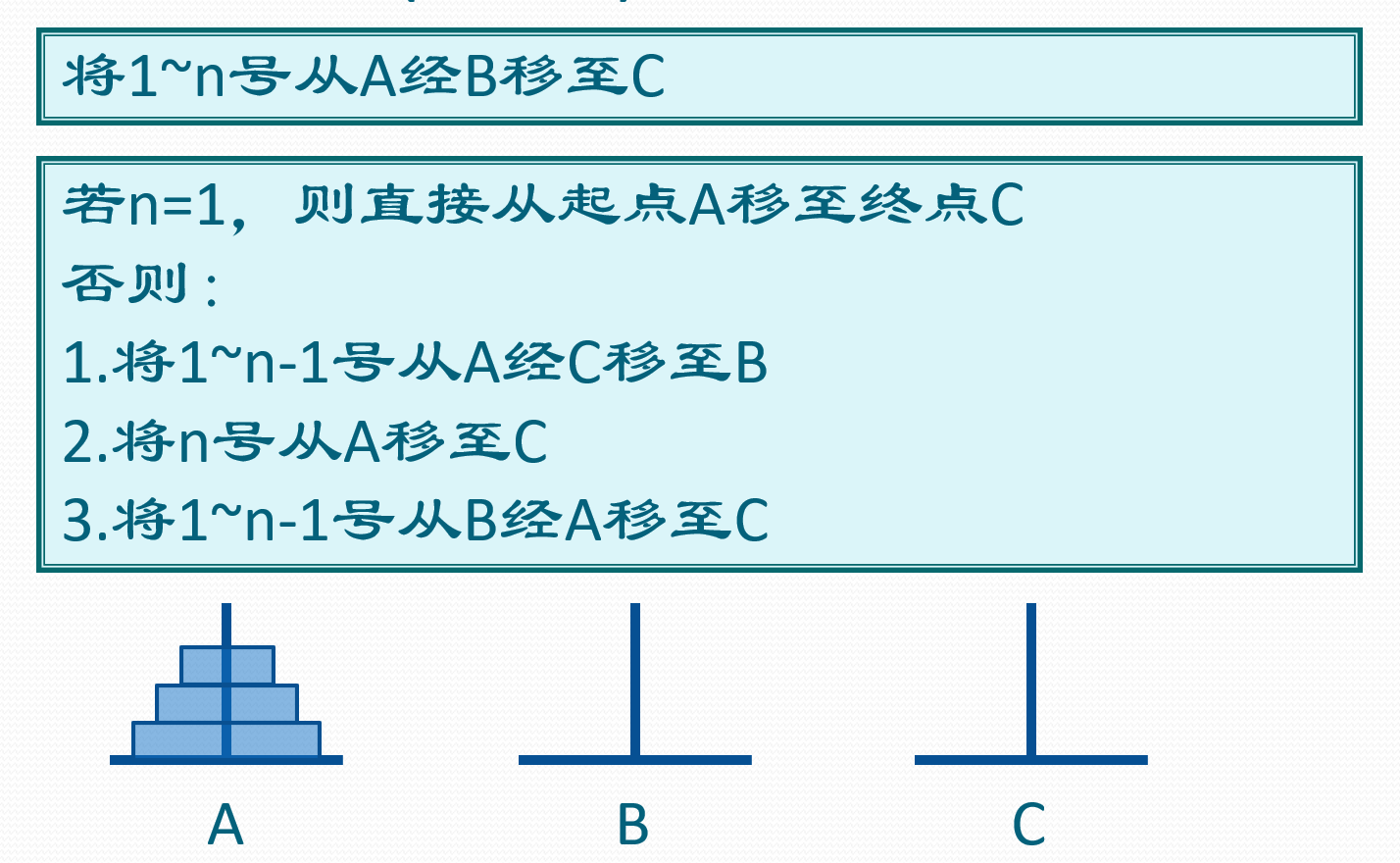
3 n阶汉诺塔

int c=0;
void move(char x,int n,char z)
{
    printf("%d.move disk%d from %c to
                      %c\n",++c,n,x,z);

}

void hanoi(int n,char x,char y,char z){  
   if(n==1)
      move(x,1,z);
   else {
     hanoi(n-1,x,z,y);
     move(x,n,z);
     hanoi(n-1,y,x,z);
   }
}

int main()
{   
     hanoi(3 ,'A','B','C');
     return 0;
}        

4 分析fun函数

//fun1函数功能：求前序遍历序列中第k个结点
#include "my.h"
#include <stdio.h>
#include <stdlib.h>

typedef char TElemType;

typedef struct BiTNode{
  TElemType data;
  struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

Status CreateBiTree(BiTree *T,FILE *fp){
  char ch;

  ch=fgetc(fp);
  if(ch=='#') *T=NULL;
  else{
    *T=(BiTNode*) malloc (sizeof(BiTNode));
    if(!*T) exit(OVERFLOW);
    (*T)->data=ch;
    CreateBiTree(&(*T)->lchild,fp);
    CreateBiTree(&(*T)->rchild,fp);
  }
  return OK;
}

Status PreOrderTraverse(BiTree T,Status (*visit)(TElemType e)){
  if(T){
    (*visit)(T->data);
    PreOrderTraverse(T->lchild,visit);
    PreOrderTraverse(T->rchild,visit);
  }
  else  return OK;
}


Status PrintElement(TElemType e){
  putchar(e);
  return OK;
}

void fun1(BiTree T,int k,BiTree *p){
  static int n=0;  
  if(T){
    n++;   
    if(n==k) {
        *p=T;     
    }    
    fun1(T->lchild,k,p);    
    fun1(T->rchild,k,p);      
  }   
  if(T)
    printf("%c ",T->data);
  else
    printf("Null ");
  printf("%d\n",n);
}

int main()
{
  BiTree T,p;
  FILE* fp;
  char ch;  

  fp=fopen("in.dat","r");
  CreateBiTree(&T,fp);
  fclose(fp);

  PreOrderTraverse(T,PrintElement);
  putchar('\n');
  fun1(T,6,&p);
  putchar(p->data);
  
  return 0; 
}

   本题先创建了一个二叉树，然后通过先序遍历输出二叉树顺序为ABDEHCFIJKG，由顺序可知第六个结点对应的结点值应该是C。
​  下面的思路就是在先序遍历过程中添加一个计数器n，若n等于k就将对应的结点地址传回去，在主函数中输出这个结点值。主要体现在fun1这个函数中。
​  在fun1中，第一次执行就是先把根节点（A）传过来，（A）结点存在计数器加一(n=1)且访问左孩子(B)，（B）结点存在计数器加一(n=2)且访问左孩子(D),（D）结点存在计数器加一(n=3)且访问左孩子（调用fun1），此时左孩子不存在，直接执行else语句输出null并输出此时的n=3。fun1函数第一次执行完。
​  返回到调用处即（D）处访问他的右孩子（调用fun1），也不存在直接执行else输出null并输出此时的n=3。fun1函数第二次执行完。
​  返回到调用处即（D）处，（D）结点存在输出结点值并输出此时的n=3，fun1函数第三次执行完。
​  返回到调用处即（B）处访问他的右孩子（E），（E）结点存在计数器加一(n=4)且访问左孩子(H)，（H）结点存在计数器加一(n=5)且访问左孩子（调用fun1），此时左孩子不存在，直接执行else语句输出null并输出此时的n=5。fun1函数第四次执行完。
​  返回到调用处即（H）处访问他的右孩子（调用fun1），右孩子不存在直接执行else输出null并输出此时的n=5。fun1函数第五次执行完。
​  返回到调用处即（H）处，（H）结点存在输出结点值并输出此时的n=5，fun1函数第六次执行完。
​  返回到调用处即（E）处访问他的右孩子（调用fun1），此时右孩子不存在，直接执行else语句输出null并输出此时的n=5。fun1函数第七次执行完。
​  返回到调用处即（E）处，（E）结点存在输出结点值并输出此时的n=5，fun1函数第八次执行完。
​  返回到调用处即（B）处，（B）结点存在输出结点值并输出此时的n=5，fun1函数第九次执行完。
​  返回到调用处即（A）处，（A）结点存在开始访问右孩子.......像以上的顺序一样访问右子树，到访问（C）时n=6=k，将（C）的地址通过形参传回主函数，最后在主函数中输出
总结：
​  1.此过程n的值是先序序列的访问顺序
​  2.每当程序fun1执行完一次，便会有内容输出，且输出内容相当于后序遍历输出每个节点值（包含空结点），以及此时有效结点数（不包含空结点）
​  3.输出规律:每次从访问到一个空的结点开始（此时有效结点数即不为空的结点数是n），到访问到下一个不为空的结点（这个结点是先序遍历中的第n+1个）或访问完 整个树（此情况是没有新结点可访问了）结束，中间fun1完成了几次执行，就输出几次n（n为第一个空的）。
例如:
​  1.第一次访问到空结点，是（D）的左孩子（n=3），下一个不为空的结点是（E），中间经过了3次执行过程，所以输出了3次3
​  2.接下来访问到空结点，是（H）的左孩子（n=5）,下一个不为空的结点是（C）,中间经过了6次执行过程，所以输出了6次5
​  3.接下来访问到空结点，是（J）的左孩子（n=9）,下一个不为空的结点是（K）,中间经过了3次执行过程，所以输出了3次9
​  4.接下来访问到空结点，是（K）的左孩子（n=10）,下一个不为空的结点是（G）,中间经过了6次执行过程，所以输出了6次10
​  5.接下来访问到空结点，是（G）的左孩子（n=11）,到访问完树结束,中间经过了5次执行过程，所以输出了5次11。